Matematik

Picard iteratione - ODE equivalent med en funcktion givet som et integrale

14. februar 2016 af SørenFr (Slettet) - Niveau: Universitet/Videregående

Jeg arbejder med differentialligning

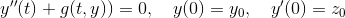
$y''(t)+g(t,y))=0, \quad y(0)=y_0, \quad y'(0)=z_0$

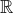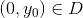hvor g er kontinuert på mængden D som er en delmængde af $\mathbb{R}$ ?, og $(0,y_0) \in D$ ?. Jeg skal vise at denne differentialligning er equivalent med

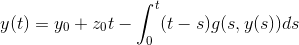
$y(t)=y_0+z_0t-\int_0^t (t-s)g(s,y(s)) ds$

Jeg bruger min differential ligning og vil interegere to gange. jeg får;

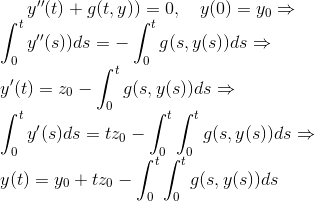
$y''(t)+g(t,y))=0, \quad y(0)=y_0 \Rightarrow \\ \int_0^{t} y''(s))ds=-\int_0^{t} g(s,y(s))ds \Rightarrow \\ y'(t)=z_0-\int_0^{t} g(s,y(s))ds \Rightarrow \\ \int_0^t y'(s)ds=tz_0-\int_0^t \int_0^{t} g(s,y(s))ds \Rightarrow \\ y(t)=y_0+tz_0-\int_0^t \int_0^{t} g(s,y(s))ds$

Det sidste double integrale giver mig et stort problem som jeg ikke ved hvordan jeg skal løse.

Brugbart svar (0)

Svar #1
14. februar 2016 af peter lind

Gør i stedet prøve. Altså finde y''(t) og y(t) for den påståede løsning og sæt resultatet ind i ligningen

Svar #2
14. februar 2016 af SørenFr (Slettet)

Det prøvede jeg også men jeg ved ikke hvordan jeg skal differentiere 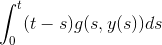$\int_0^t(t-s)g(s,y(s)) ds$

Brugbart svar (0)

Svar #3
14. februar 2016 af Therk

Per din fremgangsmåde får du at dine dobbeltintegraler mere præcist skrevet op er

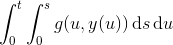
$\int_0^t \int_0^s g(u,y(u))\, \mathrm ds\, \mathrm du$

Ombyt nu integralerne ved hjælp af Fubini. Du har ikke nævnt det, men vi bliver nødt til at antage at g er en integral funktion på [0,t], ellers giver hverken dit resultat mening, og vi kan ikke bruge Fubini's sætning. Det giver

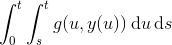
$\int_0^t \int_s^t g(u,y(u))\, \mathrm du\, \mathrm ds$

og den indre funktion er nu uafhængig af u, så det integrerer til (t-s). Se grænserne ved herunderstående:

Det er implicit antaget at 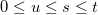fra integralerne. Det er i alt 4 uligheder:

Det første dobbeltintegrale:

$0\leq {\color{red}u} \leq s, \quad 0\leq {\color{red}s} \leq t$

Det kan vi omskrive til

$0\leq {\color{red}u}\leq t, \quad u\leq {\color{red}s} \leq t$

Svar #4
14. februar 2016 af SørenFr (Slettet)

Tak for dit svar. Jeg synes der er nogle ting du siger som er lidt mærkelige. Specielt angående dine grænser. Du siger vi får integralet

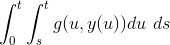
$\int_0^t \int_s^t g(u,y(u)) du \ ds$

Du siger den indre function 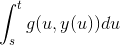$\int_s^t g(u,y(u)) du$ er uafhængig af u, og ja det er jeg enig i. Men integranten er ikke uafhænighed u. og det integere bestemt ikke til 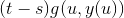(t-s) g(u,y(u)) som vi gerne vil have.

Og angående grænserne vil du så ikke gerne frem til at 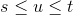$s \leq u \leq t$ for at opnå de grænser du siger?

Brugbart svar (0)

Svar #5
14. februar 2016 af Therk

Ja, det sejlede vist der - komplet vås, pånær tanken bag fremgangsmåden. Jeg byttede på et tidspunkt, under mit svar om på u og s for at stå tilbage med integratoren s, som du havde i #0. Vi prøver igen:

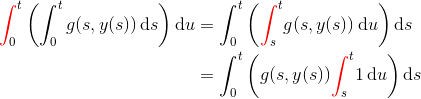
$\begin{align*} {\color{red}\int_{{\color{black}0}}^{{\color{black}t}}} \left(\int_0^t g(s,y(s))\, \mathrm ds \right ) \mathrm du &= \int_0^t \left({\color{red}\int_{{\color{black}s}}^{{\color{black}t}}} g(s,y(s))\, \mathrm du \right ) \mathrm ds \\&= \int_0^t \left(g(s,y(s)) {\color{red}\int_{{\color{black}s}}^{{\color{black}t}}} 1 \, \mathrm d u \right ) \mathrm ds \end{align*}$

og nu med farve, så vi lettere kan følge integralebyttet.

Beklager forvirringen.

Brugbart svar (0)

Svar #6
16. februar 2016 af peter lind

Du kan også omskrive integralet til t∫₀^tg(s, y(s))ds -∫₀^ts*g(s,y(s))ds

Skriv et svar til: Picard iteratione - ODE equivalent med en funcktion givet som et integrale

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.