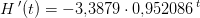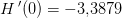Matematik

Bestem hastighed

11. marts 2009 af blazedk (Slettet)

Hej

Jeg sidder med en opgave der lyder sådan:

Afkølingen af en bestemt kop te kan beskrives ved funktionen H(t)=18+69*e^-0,0491*t

hvor t angiver antal minutter efter, at teen er blevet stillet til afkøling, og er teens
temperatur (målt i grader celsius) til tiden t.

a) Bestem teens temperatur efter 20 minutter, og bestem, hvor mange minutter, der går,
før teens temperatur er 60 grader celsius?

b) Bestem den hastighed, hvormed teens temperatur aftager efter 2 minutter.

Har fundet ud af a. Ved dog ikke hvordan man gør med b. Skal man bruge halveringskonstanten eller måske bare sige 0,0491*2???

Brugbart svar (0)

Svar #1
11. marts 2009 af Jerslev

#0: Hint til b: Differentier og bestemt H'(2).

- - -

mvh

Jerslev

Brugbart svar (0)

Svar #2
11. marts 2009 af Danielras (Slettet)

Hastigheden er H'(t). Du skal altså blot bestemme H'(2).

Svar #3
11. marts 2009 af blazedk (Slettet)

kan det så passe at man får:

H'(x)= -3,3879*(0,952086)^x

og så sætter man 2 ind på x'plads og får -3,07102?

Brugbart svar (0)

Svar #4
11. marts 2009 af Jerslev

#3: Jeps.

- - -

mvh

Jerslev

Svar #5
11. marts 2009 af blazedk (Slettet)

cool. Mange tak for hjælpen!

Brugbart svar (0)

Svar #6
12. marts 2009 af DR. Edge (Slettet)

Hej.

Jeg sidder med samme opgave, jeg har bare et spørgsmål:

Hvordan har du fundet H'(t) ? kan slet ikke finde ud af at differenciere H(t).

Brugbart svar (0)

Svar #7
05. februar 2010 af jenslindahl (Slettet)

Du bruger en lommeregner som f.eks. TI-89:

I home trykker du F3 dernæst Enter, derefter skriver du bare ligningen ind efterfulgt af ",x)"

Brugbart svar (0)

Svar #8
05. februar 2010 af mathon

TI-89

Define h(x) = 18+69*e^(-0,0491*t)

Define g(t) = d(h(t),t)

tast g(t) → -3,381·0,952086^t

.........................

manuelt
benyttes
f(x) = k·e^ax

f '(x) = k·(e^ax)' = k·e^ax·(ax)') = k·e^ax·a = (k·a)·e^ax

H'(t) = 0 + (69·(-0,0491))·e^-0,0491·t = -3,381·e^-0,0491·t
som TI-89
er programmeret til at omskrive til
-3,381·(e^-0,0491)^t = -3,381·0,952086^t

dvs
hvor
e^-0,0491 = 0,952086

Brugbart svar (0)

Svar #9
05. februar 2013 af anholt0309 (Slettet)

Hvordan udregner man opgave a?

Brugbart svar (0)

Svar #10
05. februar 2013 af Andersen11 (Slettet)

Man beregner H(20), og man skal løse ligningen H(t) = 60 .

Brugbart svar (0)

Svar #11
05. februar 2013 af anholt0309 (Slettet)

Hvordan gøres dette?

Brugbart svar (0)

Svar #12
05. februar 2013 af Andersen11 (Slettet)

#11

Man beregner H(20) vedat indsætte t = 20 i den opgivne funktionsforskrift

H(t) = 18+69*e^-0,0491*t

Dernæst skal man løse ligningen

60 = 18+69*e^-0,0491*t

Brugbart svar (0)

Svar #13
05. februar 2013 af anholt0309 (Slettet)

Okay. Tak for hjælpen :)

Brugbart svar (0)

Svar #14
12. september 2015 af snylt (Slettet)

Hvordan løser man denne ligning #12 i et CAS-program ? Har prøvet, men den vil ikke.

Brugbart svar (0)

Svar #15
12. september 2015 af mathon

CAS
          Indtast:
              Define h(t)=18+69*e^(-0.049*t)
          Beregning:
                                    h(20) <ENTER>

solve(h(t)=60,t) | t > 0

Brugbart svar (0)

Svar #16
12. september 2015 af snylt (Slettet)

mathon, jeg benytter Maple - hvordan kan man løse den via dette program?

Brugbart svar (0)

Svar #17
11. januar 2017 af Verus

#3
kan det så passe at man får:

H'(x)= -3,3879*(0,952086)^x

og så sætter man 2 ind på x'plads og får -3,07102?

Hvad betyder de -3,07102? Tak på forhånd!

Brugbart svar (0)

Svar #18
12. januar 2017 af mathon

$H{\, }'(t)=-3{,}3879\cdot 0{,}952086^{\, t}$

hvor
$H{\, }'(0)=-3{,}3879$

Brugbart svar (0)

Svar #19
13. december 2017 af mathildekri

Hvordan løser man opgaven med hvor lang tid der gør før teens temperatur er 60ºC? og opgave B uden et CAS-program, men i hånden? :)

Brugbart svar (0)

Svar #20
13. december 2017 af mathon

#19
   Du fik svar i
   https://www.studieportalen.dk/forums/thread.aspx?id=1797914

Skriv et svar til: Bestem hastighed

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.