Matematik
Komplekse tal
Hej :-)
Jeg er stødt på en opgave, som jeg har virkelig har svært ved. Jeg har prøvet at flere ting, men jeg kan ikke regne den ud.
Opgaven går ud på at beregne rødderne, og angive dem i rektangulær form:
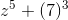
Og skal bruge følgende sætning:
![z=\sqrt[n]{\left |a \right |}e^(i(arg(a)/n+p*2pi/n))](https://media.studieportalen.dk/images/equations/Vns4LqBd-jWkDDE0z6X-Gg==.gif)
Svar #1
19. september 2014 af Andersen11 (Slettet)
Prøv at formulere, hvad der er givet, og hvad der søges. Kender man tallet w = z5 + 73 og skal så bestemme z ?
Hvis det drejer sig om at løse ligningen
z5 = a = r·eiφ
har man så
z = r1/5 · eiφ/5 · ei·p·2π/5 , p ∈ {0,1,2,3,4} .
Svar #2
19. september 2014 af Mount (Slettet)
Rødderne til polynomiet skal beregnes, samt ønskes det angivet på rektangulær form
Svar #3
19. september 2014 af Andersen11 (Slettet)
#2
Så benyt forklaringen i #1. Den polære form kan let omregnes til rektangulær form.
Svar #5
19. september 2014 af Andersen11 (Slettet)
#4
Løsningen i #1 er i polær form. Men det er jo ligetil at omregne en polær form til rektangulær form:
z = |z|·eiφ = |z|·(cos(φ) + i·sin(φ))
Svar #6
19. september 2014 af Mount (Slettet)
Men før jeg gør det, skal jeg anvende sætningen, og resultaterne laver jeg om til rektangulær form
Svar #7
19. september 2014 af Mount (Slettet)
Det er der har gjort den svær er, at der ikke er en imaginær enhed
Svar #8
19. september 2014 af Andersen11 (Slettet)
#6
Ja, beregn rødderne på polær form og omregn dem til rektangulær form.
Svar #9
19. september 2014 af Mount (Slettet)
Jeg har prøvet at anvende sætningen, men jeg får bare rigtige mange resultater på maple, mens min lommeregner ikke kan regne det ud
Svar #10
19. september 2014 af Andersen11 (Slettet)
#9
Hvis det drejer sig om ligningen
z5 + 73 = 0 eller z5 = - 73 = 73·eiπ
har man
z = 73/5 · ei(π/5 + p·2π/5) , p = 0, 1, 2, 3, 4
Svar #12
19. september 2014 af Andersen11 (Slettet)
#11
Jeg er gået ud fra dine egne oplysninger i #0. Hvis det i stedet drejer sig om en anden opgave, skal du selvfølgelig benytte de ændrede oplysninger.
Svar #13
20. september 2014 af Mount (Slettet)
Men det er sætningen der skal bruges til at beregne rødderne, hvordan har du gjort det?
Svar #14
20. september 2014 af Andersen11 (Slettet)
#13
Hvad nu end konstanten i ligningen er, kan man skrive den på formen
w5 = 1
og w er så en af de fem femte enhedsrødder ε5p = ei·p·2π/5 , p = 0, 1, 2, 3, 4 .
Svar #15
20. september 2014 af Mount (Slettet)
Forstår det ikke. Hvor bruger du så det første led af sætningen?
![\sqrt[5]{7}](https://media.studieportalen.dk/images/equations/3XgPW53_OqnjfF6H67KDXg==.gif)
Svar #16
20. september 2014 af Andersen11 (Slettet)
#15
Der er nogen tvivl om, hvordan din ligning ser ud. I #0 har du skrevet
z5 + 73 = 0
men nu tyder det mere på, at det er
z5 + 7 = 0 ?
Hvis ligningen er
z5 + k5 = 0
hvor k er et reelt tal ≠ 0, kan man skrive den på formen
(-z/k)5 = 1
hvoraf det ses, at
-z/k = ε5p = ei·p·2π/5 , p = 0, 1, 2, 3, 4
Svar #19
20. september 2014 af Mount (Slettet)
Har fundet ud af det. Hvis jeg skal skrive det på rektangulær form kan jeg så ikke anvende:
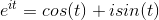



![\sqrt[5]{7}*e.....](https://media.studieportalen.dk/images/equations/ii9mvRNy_Ikh52lxhHX-aQ==.gif)
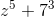
![z=\sqrt[n]{\left | a \right |}.....](https://media.studieportalen.dk/images/equations/7Jl_eikAuns7PPbKfYDXKA==.gif)
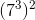
![z=\sqrt[5]{\left |343^2 \right |}e^(i((pi/2)/5+p*2pi/5))](https://media.studieportalen.dk/images/equations/53KU7NBN7yLg1FVf0xvNRA==.gif)