Matematik

Limit inferior integral, hvorfor?

01. oktober 2014 af YesMe - Niveau: Universitet/Videregående

I linket Wikipedia, står der

∫_S f dμ ≤ lim inf _n→∞ ∫_S f_n dμ, hvor følgen {f_n(s)}_n≥1 ⊂ R⁺∪{0} konvergerer punktvis mod f(s). Der oplyses generelt, fra et eller andet sted, at

lim inf _n→∞ ∫_S f_n dμ = lim _n→∞ ∫_S f_n dμ.

Her forstår jeg ikke hvorfor det er sådan som det er.

Brugbart svar (1)

Svar #1
01. oktober 2014 af Drunkmunky

Der er øjensynligt blevet brugt fatou's lemma, som er følgende:

Lad (m_n) være en følge af målelige funktioner med grænseværdi m. Da gælder, at

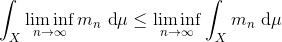
$\int_{X}\liminf\limits_{n\rightarrow\infty}m_{n}\text{ d}\mu\leq\liminf\limits_{n\rightarrow\infty}\int_{X}m_{n}\text{ d}\mu$

EDIT:

Kan se jeg misforstod dit indlæg. Du spørger om "Her forstår jeg ikke hvorfor det er sådan som det er." Det er faktisk ret enkelt. Man vil altid gerne snakke om ting, som er veldefineret, og da grænseværdien (lim) ikke altid er defineret, så bliver man nød til at benytte andre metoder, hvoraf lim inf og lim sup ALTID er defineret for reele tal, hvilke giver at de er så "gode" at bruge.

Mht. den lighed du spørger om, så gælder der, at lim eksisterer hvis og kun hvis lim sup og lim inf eksiterer.

Svar #2
01. oktober 2014 af YesMe

Tak for dit svar. Jeg har ikke nogen problemer med at forstå lemma'et. Den eneste jeg ikke forstår er det nedenstående udtryk

lim inf _n→∞ ∫_S f_n dμ = lim _n→∞ ∫_S f_n dμ.

Kender du en bog eller har et link, der fortæller noget lign. om at dette udtryk passer og hvilke krav det er, der skal opfyldes, ligesom du selv siger ".. lim eksisterer hvis og kun hvis lim sup og lim inf eksiterer."

Brugbart svar (1)

Svar #3
01. oktober 2014 af Drunkmunky

Altså det udtrykket siger er jo, at limes eksisterer, og da limes eksisterer må den være lig med limes inferior og limes superior (dette er f.eks. vist bagerst i Measures, Integrals & Martingales af René L. Schilling.)

Så vi kan formulere det på følgende måde:

Antag, at eksisterer. Da gælder, at , og det følger så af

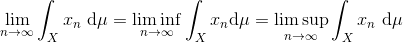
$\lim\limits_{n\rightarrow\infty}\int_{X}x_{n}\text{ d}\mu=\liminf\limits_{n\rightarrow\infty}\int_{X}x_{n}\text{d}\mu=\limsup\limits_{n\rightarrow\infty}\int_{X}x_{n}\text{ d}\mu$

Hvis du vil være helt sikker på, at det gælder så tjek enten Monoton Grænseovergangssætningen eller Lebesgues Dominerende Konvergens sætning (begge står i René L. Schillings bog).

Svar #4
01. oktober 2014 af YesMe

Mange tak for hjælpen. Hvis det er på s. 316 (under Appendix A), så forstår jeg meget bedre om grænseværdiens eksistens. Havde bare ikke læst på Appendices indtil nu.

Hvad nummer er det på deres sætninger du har nævnt om (eller evt. sidetal)?

Brugbart svar (1)

Svar #5
01. oktober 2014 af Drunkmunky

Lebesgues Dominerende Konvergens sætning er Theorem 11.2 i René L. Schillings bog (s. 90) og Monoton Grænseovergangssætningen er Theorem 11.1

Svar #6
01. oktober 2014 af YesMe

Oh well. Mange tak for svaret. Havde dog kun læst kap. 1 til 10.

Ved du forresten noget om hvorfor man f.eks. har ∫_R 1_[a,b] dλ = λ([a,b]) = λ([a, b)), hvor man har anvendt Properties 9.8 (i) til midten af udtrykket. Det højre side af udtrykket forstår jeg ikke hvorfor man ændrer sig fra ] til ). Ved du noget om det, eller kender et sted bogen forklarer om det?

Brugbart svar (0)

Svar #7
02. oktober 2014 af Drunkmunky

Det er fordi, at [a,b]=[a,b)U{b}. Og da [a,b)∩{b}=Ø, har vi, at λ([a,b])=λ([a,b)U{b})=b-a, thi {b} er en nulmængde en for lebesgue målet.

Skriv et svar til: Limit inferior integral, hvorfor?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.