Matematik

Fuldstændig løsning til differentialligning x'(t)=Ax(t)

30. oktober 2014 af joeeey (Slettet) - Niveau: Universitet/Videregående

Hej Alle :D

Jeg skal bestemme den fuldstændige løsning til differentialligning x'(t)=Ax(t)

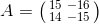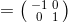
$A= \bigl(\begin{smallmatrix} 15 & -16\\ 14 & -15 \end{smallmatrix}\bigr)$ , Λ $= \bigl(\begin{smallmatrix} -1 & 0\\ 0& 1 \end{smallmatrix}\bigr)$

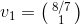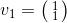
egenvektorer : $v_1= \bigl(\begin{smallmatrix} 8/7 \\ 1 \end{smallmatrix}\bigr)$ og $v_1= \bigl(\begin{smallmatrix} 1 \\ 1 \end{smallmatrix}\bigr)$

fuldstændige løsning:

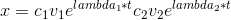
$x=c_1 v_1e^{lambda_1*t}c_2 v_2e^{lambda_2*t}$

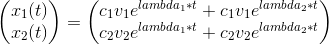
$\begin{pmatrix} x_1(t) \\ x_2(t) \end{pmatrix} =\begin{pmatrix} c_1v_1e^{lambda_1*t}+c_1v_1e^{lambda_2*t} \\ c_2v_2e^{lambda_1*t}+c_2v_2e^{lambda_2*t} \end{pmatrix}$

jeg er lidt i tvivl om man bare skal indsætte egenværdierne og egenvektorerne

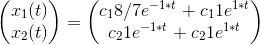
$\begin{pmatrix} x_1(t) \\ x_2(t) \end{pmatrix} =\begin{pmatrix} c_18/7e^{-1*t}+c_11e^{1*t} \\ c_21e^{-1*t}+c_21e^{1*t} \end{pmatrix}$

Hvordan finder jeg den fuldstændige løsning til x'(t)=Ax(t)???

Brugbart svar (0)

Svar #1
30. oktober 2014 af Andersen11 (Slettet)

Den fuldstændige løsning er så

x(t) = c₁·v₁·e^λ₁t + c₂·v₂·e^λ₂t

hvor v₁ og v₂ er de to egenvektorer.

Svar #2
30. oktober 2014 af joeeey (Slettet)

okay altså sådan her?:

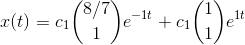
$x(t)=c_1 \binom{8/7}{1}e^{-1t}+c_1 \binom{1}{1}e^{1t}$

men skal c1 og c2 ikke også bestemmes?

Brugbart svar (0)

Svar #3
30. oktober 2014 af Andersen11 (Slettet)

Ja, det er sådan. c₁ og c₂ er vilkårlige konstanter, der kan antage alle værdier. Der er jo tale om den fuldstændige løsning.

Skriv et svar til: Fuldstændig løsning til differentialligning x'(t)=Ax(t)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.