Matematik
Partikulære løsning til differentialligningssystemet x'(t)=Ax(t) for hvilken x(0)=b
01. november 2014 af
joeeey (Slettet)
-
Niveau: Universitet/Videregående
Hej :D
jeg skal bestemme den partikulære løsning til differentialligningssystemet x'(t)=Ax(t) for hvilken x(0)=b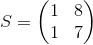 ,
, 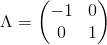 og
og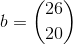
matricen 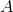 opfylder, at
opfylder, at 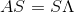
da x(0)=b kan vi skrive dette ligningssystem:
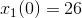
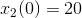
Udfra S kan vi skrive:
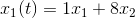
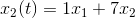 altså:
altså:
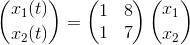
egenværdierne kan aflæses udfra 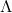 til
til 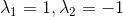 og egenvektoren til egenværdierne kan aflæses fra
og egenvektoren til egenværdierne kan aflæses fra 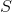 til:
til:
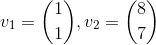
der gælder at 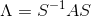 . Vi indfører hjælpefunktioner
. Vi indfører hjælpefunktioner 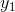 og
og 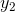
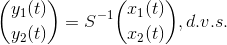
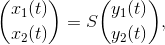 så fåes
så fåes
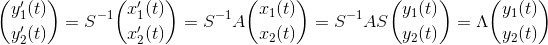 altså
altså
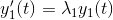 og
og 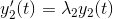 så
så
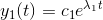 og
og 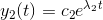 heraf følger
heraf følger
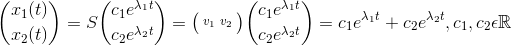 d.v.s.
d.v.s.
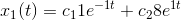
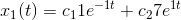
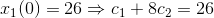
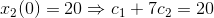
hvoraf man får 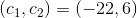
SÅ VORES PARTIKULÆRE LØSNING ER
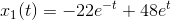
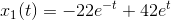
ER DET RIGTIGT ???
Skriv et svar til: Partikulære løsning til differentialligningssystemet x'(t)=Ax(t) for hvilken x(0)=b
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.









