Funktion differentiabel i et interval.

Det er i visse sammenhænge vigtigt, at en funktion er differentiabel (og derved også integrabel) i et vist interval, fordi denne/disse regneoperationer forudsættes. F.eks. ved bevisførelse, er det sommetider vigtigt at antage, at en funktion f(x) er differentiabel i et vist interval I = [a ; b], da man derved kan danne den afledte til f, altså f'(x) = dy/dx, og stamfunktionen til f, altså F(x) = ∫ f(x) dx. Formålet med at danne disse funktioner, kunne være, at man skal bruge dem senere i et bevis til f.eks. indsætning, omskrivning eller noget helt tredje, og man vil kun kunne danne disse funktioner under antagelse om, at funktionen f er differentiabel/integrabel i et givent interval - altså indenfor det interval, hvor beviset gør sig gældende (i dette tilfælde).

Men der kan sikkert også være mange andre tilfælde, hvor man bliver nødt til at være differentiabel/integrabel. Jeg skrev SRP om reaktionskinetik, hvor jeg skulle bevise sætningen om separation af de variable. I det bevis var det en nødvendighed, at jeg antog, at to funktioner g(y) og h(x) var kontinuerte og derved differentiable og integrabel på hhv. 2.- og 1.-aksen (altså skulle kontinuitet være en betingelse i det plan, som mit bevis omhandlede). Det var en nødvendighed, fordi jeg skulle danne funktionerne H(x) = ∫ h(x) dx og G(y) = ∫ 1/g(y) dy, for hvis jeg ikke kunne danne de funktioner, så kunne jeg ikke fuldføre beviset.

Håber det hjalp lidt, selvom det er lidt forvirrende :)

Hej!

Det der menes når man siger at en funktionen f(x) er differentiabel i et interval er, at grafen for f(x) er kontinuert og ikke har nogle "knæk" (hvilket vil sige ikke differentiabel).

Betragt eksempelvis:

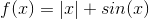
Dette er en afbildning af funktionen i intervallet fra -4 til 4, dvs.

Som du kan se har grafen et "knæk" for x = 0 og er dermed ikke differentiabel i dette punkt, (0,0).

Men grafen for f(x) er netop differentiabel i ethvert interval foruden x = 0. Dvs:

         &        

Bemærk at hvis en funktion f(x) er kontinuert, så er den ikke nødvendigvis differentiabel, men hvis en funktion er differentiabel, så vil den også være kontinuert. Med andre ord er mængden af differentiable funktioner indeholdt i mængden af kontinuerte funktioner.