Delta y altid lig med f'(x) når h går mod nul?

Det er definitionen på differentialkvotienten  f '(x₀)
Δy/Δx → f '(x₀)  for Δx → 0
Grænseværdien skal eksistere.

#1

Det er definitionen på differentialkvotienten  f '(x₀)
Δy/Δx → f '(x₀)  for Δx → 0

Og sådan er det altid uanset hvad? :-)

Sådan er det altid, hvis denne grænseværdi eksisterer.

#3

Sådan er det altid, hvis denne grænseværdi eksisterer.

Okay tak skal du have.

#3

Sådan er det altid, hvis denne grænseværdi eksisterer.

Sune, har du også forstand på buelængde? I såfald, må du meget gerne sende mig en privatbesked omkring dette. Jeg er interesseret i at vide hvorfor det er nyttigt at kende til buelængden for en funktion? Altså hvad man kan bruge denne viden til?

#5

Buelængden af grafen for en funktion f(x) mellem de to punkter (x₁ , f(x₁)) og (x₂ , f(x₂)) på grafen kan beregnes ved udtrykket

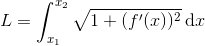
Det er selvfølgelig kun nyttigt, hvis man har brug for at kunne beregne sådanne buelængder.

#6

#5

Buelængden af grafen for en funktion f(x) mellem de to punkter (x₁ , f(x₁)) og (x₂ , f(x₂)) på grafen kan beregnes ved udtrykket

       

Det er selvfølgelig kun nyttigt, hvis man har brug for at kunne beregne sådanne buelængder.

Jeg sidder midt i en SRP og skal bevise buelængden, men kan ikke sætte den i relation til emnet omdrejningslegemer.

Hvad tænker du om det?

#7

Kan du ikke lade være med at gentage hele teksten fra det foregående indlæg, som du refererer til? Det er tilstrækkeligt at anføre indlæggets nummer, for eksempel #7.

Buelængden har ikke noget med omdrejningslegemer at gøre. Man opsummerer buelængdeelementerne

        ds = √((dx)² + (dy)²) = √(1 + (dy/dx)²) dx

hvorfor man får

        L = _x1∫^x2 ds = _x1∫^x2 √(1 + (dy/dx)²) dx = _x1∫^x2 √(1 + (f '(x))²) dx

#8

Okay tak, jeg må hellere høre min matematik lærer om hvad han har tænkt sig med buelængden.

Den er en del af min opgaveformulering.

Ha' en god aften og tak for hurtigt svar så sent. (Ps. jeg er ikke storbruger af SP, så vidste ikke det med at det var træls at man refererede til det gamle svar).

Buelængden af et kurvestykke, som roterer omkring x-aksen, kan indgå i beregningen for overfladen af omdrejningslegemet, der herved fremkommer.

Er det ikke delta S, som man kommer rundt om ved bevis for formlen af overfladearealet for et omdrejningslegeme?

#10

Ja, det var en mulighed. Så skal √(1 + (f '(x))²) så ganges med omkredsen 2π·f(x) og integreres .

#12

Jeg har allerede bevist formlen for overfladearealet, kan det så siges at buelængden er bevist internt herunder?

#13

Du har formodentlig gjort brug af buelængden af et infinitesimalt stykke af grafen i dit bevis for arealet?

#14

Jeps det tror jeg også. Rimelig vildt at have bevist buelængden uden at være bevist om det haha. Tak for hjælpen.