Matematik

Vis en mængde er lukket

28. november 2014 af ma1908 (Slettet) - Niveau: Universitet/Videregående

Jeg skal vise at mængden

$A:=\lbrace x^2 \in \mathbb{R}^2 \vert f(x)\in [a,b])$

er lukket, hvor 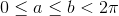$0 \leq a \leq b < 2 \pi$ . Her er funktionen f defineret ved den vinel x danner med x-aksen i positiv omløbsretning

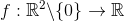
$f:\mathbb{R}^2\backslash \lbrace 0 \rbrace \to \mathbb{R}$

hvor 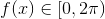$f(x)\in[0,2\pi)$ . Vinklen er entydigt givet som løsning til ligningerne

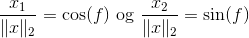
$\frac{x_1}{\Vert x \Vert_2}=\cos(f) \text{ og } \frac{x_2}{\Vert x \Vert_2}=\sin(f)$

Problemet er at funktionen f kun er kontinuert på 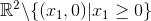$\mathbb{R}^2 \backslash \lbrace (x_1,0)\vert x_1\geq 0 \rbrace$ , så jeg ved ikke helt hvordan jeg kan argumentere for at mængden stadig er lukket. Håber nogen kan hjælpe!

Brugbart svar (0)

Svar #1
28. november 2014 af peter lind

Har du skrevet den opgave rigtig op.

f:R²\{0}->R

f er også defineret som en funktion af en vinkel d.v.s. en funktion af en variabel.

De samme problem holder for mængden A

Hvad er x1 og x2 ?

Hvad er der ellers givet om f ?

Svar #2
28. november 2014 af ma1908 (Slettet)

Undskyld, jo jeg har skrevet forkert.

$A=\lbrace x\in \mathbb{R}^2 \vert f(x)\in [a,b] \rbrace$

Her betegner x=(x₁, x₂ ). A er altså mængden af vektorer som danner en vinkel med førsteaksen som ligger mellem a og b. Er det spørgsmålet forståeligt nu?

Brugbart svar (0)

Svar #3
28. november 2014 af peter lind

Der er stadig noget galt. De udtryk for sinus og cosinus er forkerte, som du skriver det. vinklen findes som fº^-1(y) Den inverse behøver ikke engang eksistere.

For at udtrykket om begrænsningerne i definitionsmngdem skal have nogen mening må 0 betyde 0 vektoren så funktionen kun er defineret for x1≠0∧x2≠0

Du skriver at funktionen er kontinuert for de fleste værdier af x. Hvor har du det fra ?

Her har du et eksempel hvor påstanden ikke holder.

a= 0, b = 3

f(x) = 0,01+|x1+x2|)/100 for 0<|x1+x2| <1 og 0 ellers.

Med den definition vil A ikke være en lukket mængde

Svar #4
28. november 2014 af ma1908 (Slettet)

Jeg kan ikke finde fejlen, så jeg har oploaded et billede af den præcise formulering. Det er den første opgave jeg er igang med.

Vedhæftet fil:image.jpg

Brugbart svar (0)

Svar #5
28. november 2014 af peter lind

Jeg kan ikke se hvad problemet med den kontinuiteten, som du nævner sidst i #0 har med sagen at gøre. Prøv ev.t at lave et eksempel.

Randen af B består af to buer, med henholdsvis radius r og R der ligger mellem de samme to vinkler begge vinkler og dermed endepunkter inklusive.

Desuden består den af to rette linjer der går radiært ud fra (0, 0) og ligger mellem r og R igen begge endepunkter inkluderet.

Svar #6
29. november 2014 af ma1908 (Slettet)

Tak for svaret. Jeg kan sagtens følge din argumentation for at mængden er afsluttet, men jeg tror jeg skal bevise det snarere end argumentere for det. Jeg tænkte, at jeg kunne bruge at urbilledet af en afsluttet mængde under en kontinuert funktion er afsluttet, og det er derfor problemet med kontinuiteten af f opstår.

Brugbart svar (0)

Svar #7
29. november 2014 af peter lind

Funktionen ω har jo ikke noget som helst med definitionen af B at gøre, så den kan ikke bruges til at bevise at B er lukket. Jeg ved ikke hvordan du har fået defineret rand og lukket mængde eller hvilken sætninger du har lært.

Jeg har fået defineret et randpunkt som et punkt, hvor enhver omegn omkring punktet indeholder såvel punkter fra mængden og punkter udenfor mængden. Randen er så mængden af randpunkter Det er tydeligt at den rand jeg har angivet netop ifølge definitionen er rand; men du kan da godt bruge definitionen til at bevise det, hvis du har lyst.

Jeg har fået defineret, at hvis alle punkter i randen også ligger i mængden så er mængden lukket. Det fremgår også at det holder.

Skriv et svar til: Vis en mængde er lukket

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.