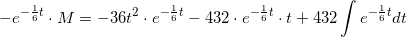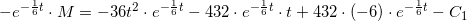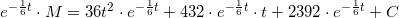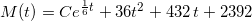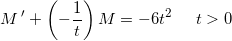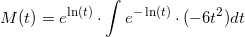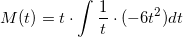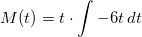Matematik
Differentialligning løses med panserformlen, eller nålestiksmetoden
Har prøvet at løse følgende differentialligning, men kan ikke få den til at give det den skal
dM/dt = 1/6 * M -6t^2
Nogle som kan hjælpe?
Svar #1
27. januar 2015 af LouiseVang (Slettet)
Ups skrev forkert, der skulle stå :
dM/dt = 1/t * M -6t^2
Svar #4
27. januar 2015 af mathon
Ændringen i #1 ændrede godt nok noget på foretagendet!
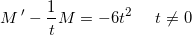 der multipliceres med
der multipliceres med  på begge sider
på begge sider
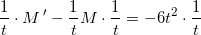
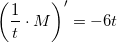 der integreres mht t på begge sider
der integreres mht t på begge sider
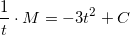
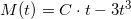
Svar #5
27. januar 2015 af LouiseVang (Slettet)
Ja undskyld fejlen :/
Men i #4 benytter du ikke panserformlen eller ? :)
Skriv et svar til: Differentialligning løses med panserformlen, eller nålestiksmetoden
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






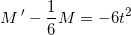 multiplicer med
multiplicer med 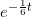
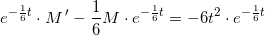
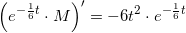 som integreres mht t på begge sider
som integreres mht t på begge sider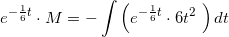
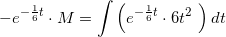
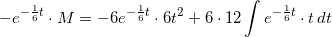
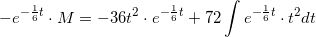
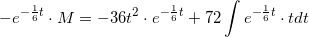
![\small -e^{-\frac{1}{6}t}\cdot M =-36t^2\cdot e^{-\frac{1}{6}t}+72\cdot \left [-6\cdot e^{-\frac{1}{6}t}\cdot t+6\int e^{-\frac{1}{6}t}\, dt \right ]](https://media.studieportalen.dk/images/equations/oALPAhsNMJ5xRv9xUqhrsg==.gif)