Optimering

Hvad er dit spørgsmål her?

Hov. Den var lige blevet klippet fra. 

Spørgsmål er: 
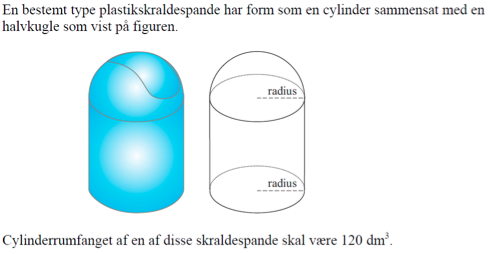
a) Indfør passende variable, og bestem radius i skraldespandens bundflade, så skraldespandens overfladeareal bliver mindst muligt. 

Opstil et udtryk for cylinderrumfanget V_cyl udtrykt ved cylinderens radius r og den højde h. Benyt

        V_cyl = 120

til at udtrykke h ved r.

Indsæt dette i et udtryk for skraldespandens overfladeareal A, og find minimum for funktionen A(r) .

VIl det sige at man indfører passende variable ved at skrive: 
Phi*r^2*h=120  
 

#4

Tallet π kaldes "pi", ikke "phi".

Man har så

         V_cyl = π·r²·h = 120 .

Opstil nu et udtryk for skraldespandens overfladeareal udtrykt ved r og h, og indsæt så det idolerede udtryk for h heri.

Er det korrekt at h=120/(pi*r^2)? 

Og skal det blot sættes ind i formlen for en cylinders overfladeareal; altså A=2*pi*r*(h+r). Eller hvordan skal udtrykket opstilles? 

#6

Der skal parentes omkring nævneren

        h = 120 / (π·r²)

Man skal have fat i hele skraldespandens areal, dvs.

        A = A(cylinder bund) + A(cylinder krum overflade) + A(låget halvkugle)

            = π·r² + 2π·r·h + 2π·r² = π·r·(3r + 2h)

Ja okay. Og i dette indsætte det isolerede h, hvorefter man finder den radius, der gør overfladearealet mindst muligt. Altså ved at løse ligningen A'(r)=0? 

#8

Ja, netop.

Kan det passe, at det giver som på billedet. I så fald - hvordan ved man om der er tale om et maksimum eller minimum? Hvis man tegner den op fremkommer to funktioner nemlig. Én med negative x-værdier og én med positive. Skal man så bare argumentere for, at udtrykket (som ses på billedet) udelukkende indeholder positive værdier og derfor MÅ være et minimum? 

#10

Jeg ved ikke, hvordan du har bestemt det udtryk. Ved at se på fortegnsvariationen for funktionen A(r) kan man afgøre, om løsningen til A '(r) = 0 angiver et lokalt minimum eller lokalt maksimum.

Jeg havde glemt at afrunde resultatet. Det kan godt passe, at det giver 2,335 ikke? Det passer ihvertfald, hvis man tegner A(r) op. 

#12

Igen: Jeg ved ikke, hvor du har det tal fra.