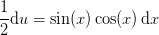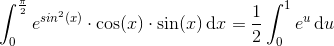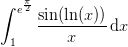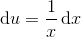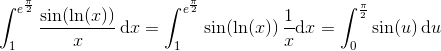Matematik
Bestemte integraler
Hej
Jeg kan ikke finde ud af følgende to bestemte integraler:
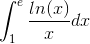
og
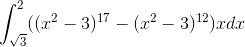
Har prøvet at anvende integration med substitution, men jeg kommer ikke rigtig nogle vejne.
Håber, at det der en, som vil hjælpe.
På forhånd tak
Svar #3
24. april 2015 af NTNTNTNT (Slettet)
Mange tak for hjælpen.
Mit problem med denne type opgaver er, at jeg har vanskeligt ved at bestemme den indre funktion. Når først jeg har gjort dette, er det relativt nemt for mig at løse opgaverne. Hvordan afgører du, hvad den indre funktion er?
Svar #4
24. april 2015 af Toonwire
#3
Det handler ofte om at gennemskue (kommer med erfaring) hvad der kan substitueres og derefter differentieres således, at man kan simplificere udtrykket.
I de fleste tilfælde kan slippe afsted med at vælge den indre funktion når man snakker sammensatte funktioner.
Svar #5
24. april 2015 af mathon
Anvendelse af substitution i forbindelse med integralregning
kræver et integral af typen
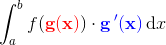
Den indre funktions afledede skal stå som faktor (blå).
Med
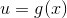 og dermed
og dermed 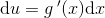
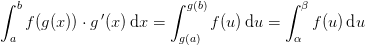
Rutineret kendskab til parrene
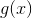
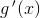 hjælper meget.
hjælper meget.
Svar #6
24. april 2015 af Andersen11 (Slettet)
Det første integral kan også beregnes ved partiel integration, idet man har
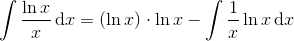
hvoraf man ser, at
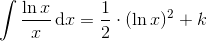
Svar #7
25. april 2015 af NTNTNTNT (Slettet)
Tak for svarene de er meget brugbare, men nu har jeg forsøgt at bestemme den indre funktion i følgende stykker uden held:
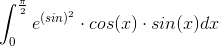
og
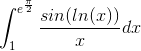
Hvad er jeres bud der?
Skriv et svar til: Bestemte integraler
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.









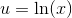 og dermed
og dermed 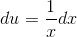
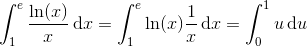
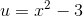 og dermed
og dermed 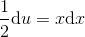
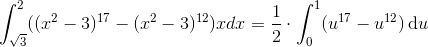
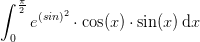
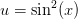 og dermed
og dermed