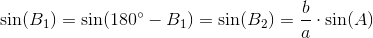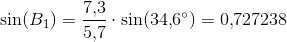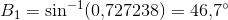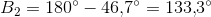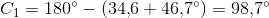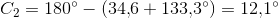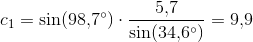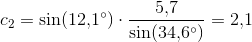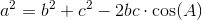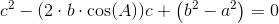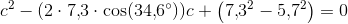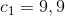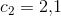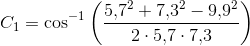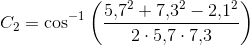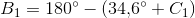Matematik
Sinusfælden!?
Har været så "heldig" at trække mundtlig matematik til eksamen, hvor jeg har fået opgaven:
Redegør for begrebet "sinusfælden" og hvad det betyder for brugen af sinusrelationerne
Jeg har lidt svært ved at finde ud af hvad jeg skal bevise. Håber nogen kan hjælpe!
Vh
Svar #1
02. juni 2015 af LeonhardEuler
At der til et givent trigonometrisk problem vil eksistere uendelig mange vinkler x, der opfylder sinusrelationen eller to for 0 ≤ x ≤ 180. Betragt enhedscirklen - det er et gyldigt bevis.
Svar #2
02. juni 2015 af mathon
For vinklerne  i en trekant
i en trekant
![v\in \left [ \, 0\; ;180^{\circ} \right ]](https://media.studieportalen.dk/images/equations/0DEFJ_vgjG6nwE9g6Nb6ng==.gif)
gælder
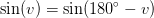
dvs ligningen
![\sin(v)=a\; \; \; \; a\in \left [ -1;1 \, \right ]](https://media.studieportalen.dk/images/equations/HEs48OzA6_tMiLQUUV34CQ==.gif)
har 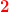 løsninger
løsninger
medens
![\cos(v)=a\; \; \; \; a\in \left [ -1;1 \, \right ]](https://media.studieportalen.dk/images/equations/T8gYwMg6jQ9iPjVxa80tmg==.gif)
har 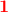 løsning.
løsning.
.........
Vinkelberegning ved anvendelse af sinusrelationer er derfor ikke i alle tilfælde éntydig,
medens cosinusrelationen altid giver en éntydig vinkel.
Svar #3
02. juni 2015 af LeonhardEuler
Benyt følgende sætning:
I en vilkårlig trekant vil den største side ligger overfor den største vinkel, og tilsvarende vil den mindste side ligge overfor den mindste vinkel.
Svar #4
02. juni 2015 af SuneChr
"Sinusfælden" ligger i beregningen af en trekant, hvor en vinkel, en hosliggende side og vinklens modstående side er givne.
Svar #5
03. juni 2015 af Imsmart (Slettet)
Jeg er meget forvirret over de mange forskellige svar. Hvad ville passe bedst at tegne og fortælle til en eksamen? Jeg har lidt svært ved at forstå det
Svar #7
03. juni 2015 af Jacobadm (Slettet)
Du kan også læse om sinusfælden eller det dobbelttydige tilfælde i artiklen Trekantsberegning i vores Matematik formelsamling.
Skriv et svar til: Sinusfælden!?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


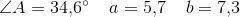
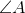 er spids og
er spids og 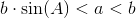
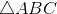 to løsninger.
to løsninger.