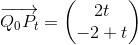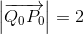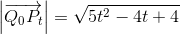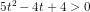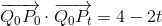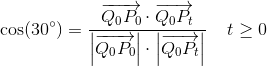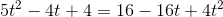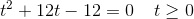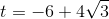Matematik
Vektor og plangeometri
Hej SP
Nogen der kan lave det her, da jeg virkelig er på bar bund. Tak på forhånd!
Svar #1
06. oktober 2015 af mathon
I trekant 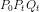
er:
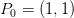
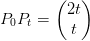
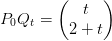
Arealet af 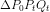
er det halve af determinantens numeriske værdi:
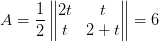
hvoraf
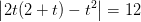
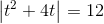
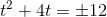
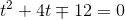
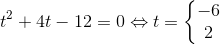
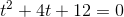 har ingen reelle løsninger.
har ingen reelle løsninger.
Arealet af 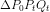 er 6
er 6
for 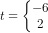
Svar #2
06. oktober 2015 af mathon
korrektion:
I trekant 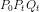
er:
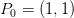
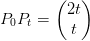
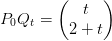
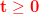
Arealet af 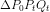
er det halve af determinantens numeriske værdi:
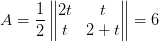
hvoraf
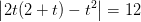
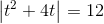
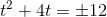
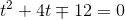
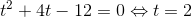
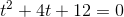 har ingen reelle løsninger.
har ingen reelle løsninger.
Arealet af 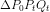 er 6
er 6
for 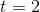
Skriv et svar til: Vektor og plangeometri
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





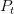 og
og 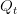 har hældningskoefficienten
har hældningskoefficienten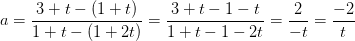
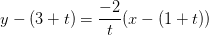
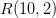 ligger på linjen,
ligger på linjen,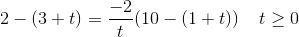
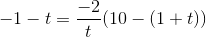 multipliceres med
multipliceres med 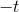
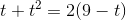
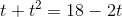
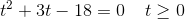
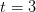
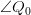 er vinklen mellem vektorerne
er vinklen mellem vektorerne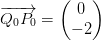 og
og