Matematik
Topologi hjælp med en opgave
Hej jeg har en opgave jeg simpelhen ikke kan løse håber der er en der kan hjælpe!
Lad (X,d) være et metrisk rum og x in X et element i X. Vis at
{ y \in X | d(y,x) > r } for alle r \in R (realle tal)
Svar #2
07. februar 2016 af Janee (Slettet)
#1Selve spørgsmålet mangler?
Hej jeg har en opgave jeg simpelhen ikke kan løse håber der er en der kan hjælpe!
Lad (X,d) være et metrisk rum og x in X et element i X. Vis at
{ y \in X | d(y,x) > r } er åben for alle r \in R (realle tal)
Sådan håber det giver mere mening. beklager
Svar #3
07. februar 2016 af VandalS
Jeg kan starte med at give et hint: Lad der være givet et metrisk rum 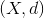 . Et sæt
. Et sæt 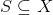 er åbent hvis der til ethvert punkt
er åbent hvis der til ethvert punkt 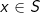 kan indlægges en åben kugle
kan indlægges en åben kugle 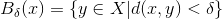 med centrum i
med centrum i  og radius
og radius 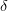 således at
således at 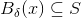 . Til denne opgave ville et smart valg være
. Til denne opgave ville et smart valg være 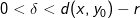 , hvor
, hvor 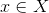 er vilkårligt og
er vilkårligt og 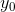 er et andet vilkårligt punkt hvorom der gælder at
er et andet vilkårligt punkt hvorom der gælder at 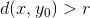 .
.
Svar #4
07. februar 2016 af Janee (Slettet)
Tusind tak for dit svar Vandal. Men det er ligepræsis der jeg sidder fast ! for y0 ligger vel i komplementat mængden altså uden for S. Men jeg har ingen anelse om hvordan jeg skal betegne Komplementarmængden udover SC. Vil gerne have den matematiske form... Eller er jeg helt galt på den?
Svar #5
07. februar 2016 af Janee (Slettet)
Eller r skal vel bare være mindre end x0-y0? så er den vel hjemme
Svar #6
07. februar 2016 af VandalS
Hvis 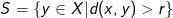 så er
så er 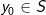 fordi vi kræver at
fordi vi kræver at 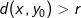 , som jo er kravet for at være et element i
, som jo er kravet for at være et element i 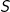 . Jeg ville angribe opgaven på den måde jeg har foreslået, men alternativt kunne det også gøres ved at vise at komplementærmængden
. Jeg ville angribe opgaven på den måde jeg har foreslået, men alternativt kunne det også gøres ved at vise at komplementærmængden 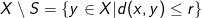 er lukket hvis du finder det nemmere.
er lukket hvis du finder det nemmere.
Svar #7
07. februar 2016 af Janee (Slettet)
Årrrh jamen jeg forstår ikke helt hvad der mangler for at løse opgaven? For kan godt følge din tankegang og det gav meget mere mening. Men jeg kan ikke se andet en det må gælde for alle y in S eksitere der [\delta] >0 så [B_{\delta}(x) \subseteq S] . Jeg kan virkelig ikke se hvad der mangler for at løse opgaven mere? Den er vel løst så med din forklaring? jeg vil vel bare betegne at r skal være mindre end den numeriske difference mellem x_0 og y_0
Svar #8
07. februar 2016 af VandalS
Det er ikke nok i matematik at sige at "der må gælde."
Vi er givet et metrisk rum 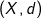 , et punkt
, et punkt 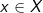 og en radius
og en radius 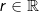 . Definér
. Definér 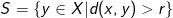 .Så skal der for at løse opgaven med min fremgangsmåde vises at:
.Så skal der for at løse opgaven med min fremgangsmåde vises at:
1) Der eksisterer et 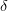 således at
således at 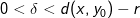 .
.
2) For et vilkårligt punkt 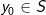 skal det vises at
skal det vises at 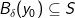 , det vil sige at ved hjælp af trekantsuligheden skal det vises at for et vilkårligt
, det vil sige at ved hjælp af trekantsuligheden skal det vises at for et vilkårligt 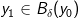 gælder der at
gælder der at 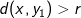
Svar #9
07. februar 2016 af Janee (Slettet)
Jeg tror virkelig jeg har kigget på den her opgave for længe så jeg er blevet blind... Jeg tror næsten hvis du kan løse den, må du meget gerne det, så kan jeg nok bedre forstå hvordan det skal gøres, for lige nu sidder jeg på den 13 time med den her opgave og jeg forstår simpelthen ikke metoden selvom jeg læser bogen igennem 100 gange. Det ville være pisse fedt hvis du gav, så kan jeg sove trygt inat og kigge på forståelsen af metoden imorgen og forhåbelig selv løse den slags opgaver fremover!
Svar #10
07. februar 2016 af VandalS
Helt i orden. Jeg skriver et svar med mit løsningsforslag, og bagefter et svar med uddybende forklaring og motivering.
Svar #11
07. februar 2016 af VandalS
Vi er givet et metrisk rum 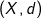 , et punkt
, et punkt 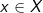 og et tal
og et tal 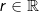 . Definér
. Definér 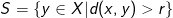 . Vi skal vise at
. Vi skal vise at 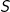 er en åben mængde. Dette er per definition tilfældet hvis vi for ethvert vilkårligt punkt
er en åben mængde. Dette er per definition tilfældet hvis vi for ethvert vilkårligt punkt 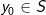 kan indlægge en åben kugle
kan indlægge en åben kugle 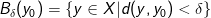 således at
således at 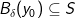 .
.
Vælg derfor ![\delta \in \]0;d(x,y_0)-r \[](https://media.studieportalen.dk/images/equations/FEvQlyUPux-Niwqoa5ZlPw==.gif) ; dette tal er veldefineret idet der per antagelse gælder at
; dette tal er veldefineret idet der per antagelse gælder at 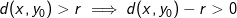 , så intervallet er ikke-tomt.
, så intervallet er ikke-tomt.
Lad 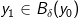 være et vilkårligt punkt i den åbne kugle med centrum i
være et vilkårligt punkt i den åbne kugle med centrum i 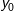 og radius
og radius 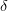 . Et sådan punkt findes da
. Et sådan punkt findes da 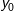 opfylder betingelserne.
opfylder betingelserne.
Da 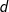 er en metrik opfylder den trekantsuligheden og er symmetrisk i de to indgange, og derfor har vi at
er en metrik opfylder den trekantsuligheden og er symmetrisk i de to indgange, og derfor har vi at 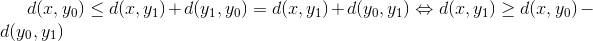
Per vores valg af 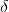 gælder der at
gælder der at 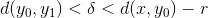 , hvilket medfører at
, hvilket medfører at 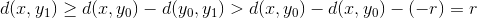 . Dermed har vi vist at
. Dermed har vi vist at 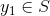 , og da
, og da 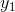 var vilkårligt valgt i
var vilkårligt valgt i 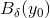 har vi dermed vist at
har vi dermed vist at 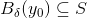 som ønsket. Q.E.D.
som ønsket. Q.E.D.
Svar #12
07. februar 2016 af VandalS
Jeg kan godt forstå at det med topologi er svært. Jeg havde også problemer med det i starten - ofte følte jeg at der skulle et "hokus-pokus" trick til for at få det til at gå op, men det kommer med erfaring.
Med en opgave som denne vælger jeg den tilgang jeg har benyttet ovenfor fordi jeg af erfaring ved at det ofte kan løses ved at benytte trekantsuligheden på den rigtige måde. For at kunne vise det vi vil skal vi have fat i de tre punkter 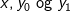 , hvilket giver anledning til de tre afstande
, hvilket giver anledning til de tre afstande 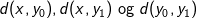 . Den første er givet i opgaven, den anden er den vi ønsker at vise er større end
. Den første er givet i opgaven, den anden er den vi ønsker at vise er større end  og dermed vise at
og dermed vise at 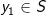 , og den tredje kan vi kontrollere med vores valg af
, og den tredje kan vi kontrollere med vores valg af 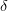 .
.
Vi skal nu bruge trekantsuligheden til at manipulere de tre afstande til et udtryk der fortæller os noget om den ønskede længde 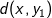 . Vi kan benytte trekantsuligheden på hver af de tre afstande, men to af de tre giver os ikke noget brugbart. Den vi kan bruge til noget er
. Vi kan benytte trekantsuligheden på hver af de tre afstande, men to af de tre giver os ikke noget brugbart. Den vi kan bruge til noget er 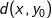 , hvor vi indskyder punktet
, hvor vi indskyder punktet 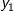 og får
og får 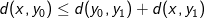 , hvori vi isolerer
, hvori vi isolerer 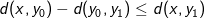 . Nu gælder det om at vælge
. Nu gælder det om at vælge 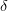 rigtigt så vi kommer frem til den ønskede ulighed
rigtigt så vi kommer frem til den ønskede ulighed 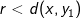 .
.
Dette er rigtigt hvis vi opfylder at 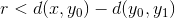 , som vi kan sikre ved lidt manipulation:
, som vi kan sikre ved lidt manipulation:
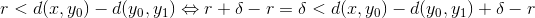
Da der per definition gælder at 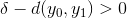 kan vi opfylde dette ved at benytte det strengere krav
kan vi opfylde dette ved at benytte det strengere krav 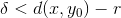 . Herefter er det bare et spørgsmål om at vise at dette valg er veldefineret og indsætte dette i de gamle udtryk for at vise at opgaven er løst.
. Herefter er det bare et spørgsmål om at vise at dette valg er veldefineret og indsætte dette i de gamle udtryk for at vise at opgaven er løst.
Håber det giver mening =)
Svar #14
07. februar 2016 af VandalS
Vi har ikke benyttet udregninger der kræver at  er et positivt tal, så
er et positivt tal, så  kan være nul (eller negativ) uden problemer. Hvis
kan være nul (eller negativ) uden problemer. Hvis  er negativ opfylder hele
er negativ opfylder hele 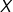 kravet til at være i
kravet til at være i 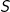 , hvilket ikke er et problem da hele "universet"
, hvilket ikke er et problem da hele "universet" 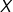 i et metrisk rum per definition er både åbent og lukket. Hvordan
i et metrisk rum per definition er både åbent og lukket. Hvordan 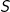 skal forstås når
skal forstås når 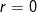 afhænger af metrikken.
afhænger af metrikken.
Skriv et svar til: Topologi hjælp med en opgave
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







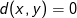 er
er 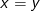 , så
, så 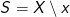 , og da
, og da