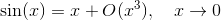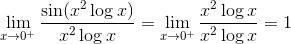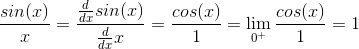Matematik
Grænseværdi: Har brøken en grænseværdi
Jeg vil gerne have hjælp til at bevise med epsilon -delta definition af grænseovergang om brøken
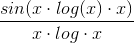
har en grænseværdi for 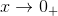
på forhånd tak
Svar #5
13. februar 2016 af StoreNord
.. og også fra venstre. Men jeg ved ikke hvordan man beviser det. :)
Svar #7
13. februar 2016 af SuperManBat
jeg er ikke helt med mathon
hvordan skal jeg skal jeg bruge 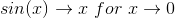
for at bevise at grænseværdien er 1
Skriv et svar til: Grænseværdi: Har brøken en grænseværdi
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



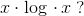
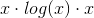
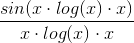 har grænseværdien 1 ifølge Geogebra.
har grænseværdien 1 ifølge Geogebra.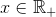
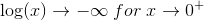
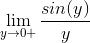
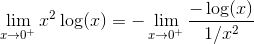
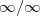 "-udtryk. Anvend L'Hopital og se at udtrykket har grænseværdi 0. En taylorudvikling på sinus omkring nul (vi skal have argumenteret for ovenstående før dette giver mening!) giver
"-udtryk. Anvend L'Hopital og se at udtrykket har grænseværdi 0. En taylorudvikling på sinus omkring nul (vi skal have argumenteret for ovenstående før dette giver mening!) giver