Matematik
en funktion f er givet ved f(x)=x^3+x-2
Hejsa.
nogen der kan hjælpe mig med denne nedenstående opgave?
en funktion f er givet ved
f(x)=x^3+x-2
a) bestem f'(x), og gør vedhjælp heraf rede for, at f er voksende.
Nogen der kan forklare trinene for mig?
Tretrinsreglen anvendes.
Funktionstilvæksten 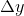 for det første led x^3 findes:
for det første led x^3 findes:
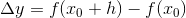
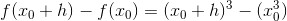
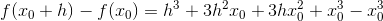
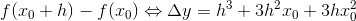
Differenskvotienten (sekanthældningen) findes:
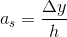
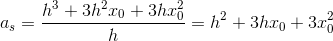
Til sidst findes differentialkvotienten (tangentens hældning) ved at tage grænseværdien af differenskvotienten, når h går mod 0:
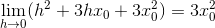
Differentialkvotienten findes på samme måde ved at bruge tretrinsreglen for de resterende to led x og -2, her først x:
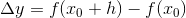
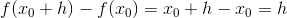
Differenskvotienten:
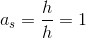
Differentialkvotienten:
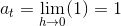
På samme måde gøres det for det sidste led -2:
Funktionstilvæksten:
Da der ikke er noget x i det sidste led, bliver differentialkvotienten tydeligvis 0, fordi man ikke kan indsætte noget på x'es plads.
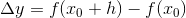
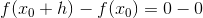
Differenskvotienten:
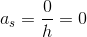
Differentialkvotienten:
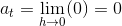
Dermed har man for den samlede funktion, at:
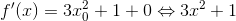
Som #1 siger, er f voksende, fordi 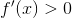 (altså tangentens hældning) for alle reelle tal, da et hvilket som helst reelt tal i anden giver en positiv værdi.
(altså tangentens hældning) for alle reelle tal, da et hvilket som helst reelt tal i anden giver en positiv værdi.
#2På samme måde gøres det for det sidste led -2:
Funktionstilvæksten:
Da der ikke er noget x i det sidste led, bliver differentialkvotienten tydeligvis 0, fordi man ikke kan indsætte noget på x'es plads.
Hovsa, her kom jeg vist lige til at lave en fejl. Resultatet giver dog det samme. Der skulle selvfølgelig have stået
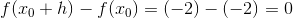
Skriv et svar til: en funktion f er givet ved f(x)=x^3+x-2
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





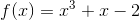
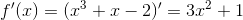
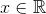 dermed er
dermed er 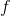 voksende
voksende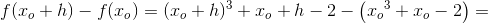
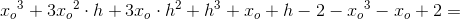
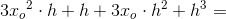
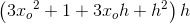
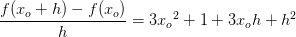
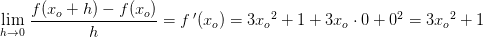
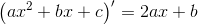 som anvendt i #1
som anvendt i #1 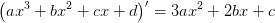 som anvendt i #1
som anvendt i #1