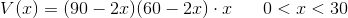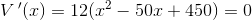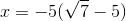Matematik

Optimering af volumen af en kasse

24. juli 2016 af hk01 - Niveau: B-niveau

Hej jeg vil bare tjekke om min løsning af dette spørgsmål er rigtigt, håber nogle kan hjælpe med det.

Jeg vedhæfter spørgsmålet og min løsning.

Svar #1
24. juli 2016 af hk01

Spørgsmål

Svar #2
24. juli 2016 af hk01

Løsning

Svar #3
24. juli 2016 af hk01

Jeg kan ikke vedhæfte filen, så beskriver spørgsmålet:

En rektangulær plade på 60 x 60 cm²skal benyttes til at lave en kasse uden låg. Dette gøres ved at skære et kvadrat med sidelængde x væk fra hvert hjørne af pladen og derefter folde siderne op, så der opstår en kasse.

Bestem den sidelængde x af kvadraterne, der giver det størst mulige rumfang af kassen.

Der er vist en illustration også, hvor højden af kassen er defineret som x. Kan desværre ikke vedhæfte det af en eller anden årsag.

Svar #4
24. juli 2016 af hk01

Min løsning:

Jeg definerer længde, bredde og højde:

L = 90-2x

B = 60-2x

H = x

Rumfang som funktion af x:

R(x) = (90-2x)(60-2x)x

solve(R'(x) = 0,x)

x = 38.2 cm

Er dette rigtigt, er der en der kan hjælpe mig i den rigtige retning hvis det er forkert?

Svar #5
24. juli 2016 af hk01

Jeg prøvede igen med opgaven, og jeg kan nu se at løsningen 38.2 ikke giver mening da rumfanget så bliver et negativt tal. Da diskriminanten giver et tal højere end nul, er der 2 løsninger, og den anden løsning er 11.8, hvilket giver mere mening.

Brugbart svar (1)

Svar #6
25. juli 2016 af Capion1

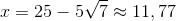
$x=25-5\sqrt{7}\approx 11,77$
x skal nødvendigvis være mindre end 30, da 60 - 2x > 0
Kassen rummer da 28520,259 cm³ eller godt og vel 28¹/₂ dm³

Brugbart svar (1)

Svar #7
25. juli 2016 af mathon

En rektangulær plade på 60 x 60 cm²
af skæres et kvadrat med siden x i de 4 hjørner,

hvoraf
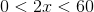
   0<2x<60
    0<x<30

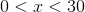
kassens bund er kvadratisk med siden 60-2x og højden x

kassens volumen:
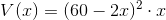
$V(x)=(60-2x)^2\cdot x$
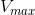$V_{max}$ kræver
$V{\, }'(x)=0$

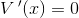
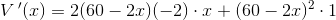
$V{\, }'(x)=2(60-2x)(-2)\cdot x+(60-2x)^2\cdot 1$

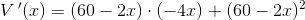
$V{\, }'(x)=(60-2x)\cdot (-4x)+(60-2x)^2$

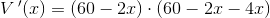
$V{\, }'(x)=(60-2x)\cdot(60-2x-4x)$

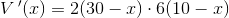
$V{\, }'(x)=2(30-x)\cdot6(10-x)$

krav:

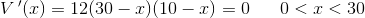
$V{\, }'(x)=12(30-x)(10-x)=0\; \; \; \; \; \; 0<x<30$
dvs:
   fortegnsvariation for
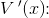   $V{\, }'(x)\! \! :$ + 0 -
   0_______10____________30
monotoni for max
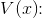   $V(x)\! \! :$   ^voksende ^aftagende

konklusion:

Den sidelængde x af kvadraterne, der giver det størst mulige rumfang af kassen
er:
   x=10

Svar #8
25. juli 2016 af hk01

#7 jeg har ved en fejl skrevet 60 x 60 tidligere. Det er 60 x 90.

Brugbart svar (1)

Svar #9
25. juli 2016 af mathon

OK!
$V(x)=(90-2x)(60-2x)\cdot x\; \; \; \; \; \; 0<x<30$

krav:
$V{\, }'(x)=12(x^2-50x+450)=0$

$x=-5(\sqrt{7}-5)$

Svar #10
25. juli 2016 af hk01

Tak for hjælpen til jer begge to. Jeg kom frem til det samme resultat.

Skriv et svar til: Optimering af volumen af en kasse

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.