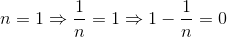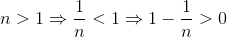Matematik
Matematik: Mændelære (uni begynder)
Hej søde lektiehjælpere!
Jeg har denne opgave:
 En der kan hjælpe mig med at bevise dem? Jeg har regnet frem, at:
En der kan hjælpe mig med at bevise dem? Jeg har regnet frem, at:
(7):

(8):

Min underviser mener dog, at jeg skal bevise det og ikke lave eksempler på, at det passer. Hvordan kan jeg gøre det? Min lærebog er knap så god til at hjælpe.
På forhånd tak!
Svar #1
25. oktober 2016 af Therk
Undlad gerne at skrive "haster" i din overskrift. Du vil vel ikke lade det virke som om din tid er vigtigere end vores? :)
Svar #5
25. oktober 2016 af KaspermedK
Tak for svar. Kan du uddybe?
Jeg tror det er:

Jeg er sikkert nok på vild spor..
Svar #7
25. oktober 2016 af Therk
Right. Fjern limes. Hvad ved du om den disjunkte mængde for k = 1? Hvad med k = 2? Og for et vilkårligt k? Med svar på de spørgsmål, hvad sker der, når du så tager grænseværdien på igen? Hint: Se svar #4.
Svar #8
25. oktober 2016 af KaspermedK
Jeg ved, at A∩B=Ø, så er A og B disjunkte. Men for k=1 så er det vel den maksimale værdi den kan nå? Dvs.

Dvs.
![A_{1} = [-1;0]](https://media.studieportalen.dk/images/equations/KIHyTSjgYzUFTn0t1oXbng==.gif)
For k=1 jo. Hvis k=2 kan n være både 1 og 2?
Svar #9
25. oktober 2016 af Therk
Ja. Og hvad er
![\bigcap_{n = 1}^2 A_n = A_1 \cap A_2 = [-1;1-1]\cap [-1;1-1/2]](https://media.studieportalen.dk/images/equations/szWRoyHMyggeQ6a9BtwM_w==.gif)
? Kan du fortsætte?
Kan du sige noget om hvordan A1 og A2 forholder sig til hinanden? Er den ene en delmængde af den anden? Hvad med A1 og Ak for et vilkårligt k?
Svar #10
25. oktober 2016 af Eksperimentalfysikeren
Om den første:
An = [-1;1-1/n] . Da 1/1 > 1/n for alle n større end 1, er 1-1/1 = 0 den mindste øvre grænse for intervallerne og da de har samme nedre grænse, gælder der at An⊂Am for n<m. Fællesmængden af to mængder, B og C, for hvilke det gælder, at B ⊂ C er lig B. Derfor er den angivne fællesmængde lig med A1.
Svar #11
25. oktober 2016 af KaspermedK
Okay, jeg siger k=3, så er

Og jeg ved godt, at hvis vi sender k mod uendeligt, så må vi jo få det jeg påstår, nemlig [-1;0], men hvordan skal jeg skrive det op? Har leget lidt med noget her:
Forresten al respekt til jer at hjælpe mig!
Svar #12
25. oktober 2016 af Therk
Og du er bestemt på rette vej, men ja, du mangler lige det afgørende argument. Problemet er måske her at din underviser har taget ret trivielle mængder. Anyways, lad os prøve at få det formelle argument på plads.
Er der et af følgende udsagn, der er sandt? Hvad sker der med sådanne mængder, når du tager fællesmængde og forening?
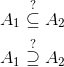
Svar #13
25. oktober 2016 af KaspermedK
Den øverste
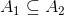
Må altså være for foreningsmængden, hvoraf
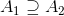
Må være fællesmængden. Hvorfor? Fordi 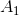 er den mindste værdi man kan antage? Hvor i foreningsmængden må det være (i følge dine udsagn)
er den mindste værdi man kan antage? Hvor i foreningsmængden må det være (i følge dine udsagn) 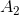
Håber det gav mening.
Svar #14
26. oktober 2016 af Therk
Hmm, det er ikke helt rigtigt forstået af subset-tegnet. 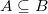 betyder at A er en delmængde af B og derved at ethvert element i A også ligger i B.
betyder at A er en delmængde af B og derved at ethvert element i A også ligger i B.
Vi er så heldige i denne opgave at
![A_1 = [1;1-1] \subseteq [1;1-1/2] = A_2](https://media.studieportalen.dk/images/equations/F-pl4ygTmr6wzWZdOmTYcQ==.gif)
Men fællesmængden af to mængder, hvoraf den ene mængde er i den anden mængde er blot den mindste mængde. Dvs. symbolsk,

og generelt, for ethvert k>j gælder der i vores tilfælde at
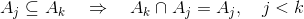
Den sidste linje er sådan set nok til at sige at fællesmængden af alle A'erne er A1 = [1;0].
Du kan evt. erstatte A'erne med de mængder, der repræsenterer, hvis du hellere vil det.

Til foreningsmængderne, lav samme type observation. Mængderne forholder sig stadig på samme måde ift. hinanden, men nu gælder der at 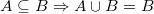 . Så denne gang skal du lade k løbe mod uendeligt for at finde den fulde mængde! Dvs. argumentér på samme måde som ovenstående og find
. Så denne gang skal du lade k løbe mod uendeligt for at finde den fulde mængde! Dvs. argumentér på samme måde som ovenstående og find
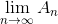
(som du allerede gjorde i #0).
Svar #15
26. oktober 2016 af AskTheAfghan
Lad An = [-1, 1 - 1/n] for alle n≥1. For at vise ∩n∞An ⊆ [-1,0], dvs. hvis x∈∩n∞An, så er x∈[-1,0], kan du vise det ved kontraposition, at hvis x∉[-1, 0], så er x∉∩n∞An. Benyt definitionen for ∩n∞An, og du er færdig (hvorfor?). For den omvendte inklusion, er det ret let at vise. Prøv.
Svar #16
02. november 2016 af Eksperimentalfysikeren
A1∩A2 = A1 eller mere detailleret:
![\left [ -1;1-\frac{1}{1} \right ]\cap \left [ -1;1-\frac{1}{2} \right ] =\left [ -1;0 \right ]\cap \left [ -1;\frac{1}{2} \right ] = \left [ -1;0 \right ]](https://media.studieportalen.dk/images/equations/5gcjMlZIo524ug6ukzXeVQ==.gif)
A1∩A3 = A1 eller mere detailleret:
![\left [ -1;0 \right ]\cap \left [ -1;1-\frac{1}{3} \right ] =\left [ -1;0 \right ]\cap \left [ -1;\frac{2}{3} \right ] = \left [ -1;0 \right ]](https://media.studieportalen.dk/images/equations/awmubq0YM1SXFmY6tXcNDg==.gif)
Hvert trin giver den samme fællesmængde, så det gør ∩n=1∞An også.
Skriv et svar til: Matematik: Mændelære (uni begynder)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






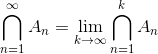
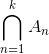
![\bigcap_{n=1}^{\infty }A_{n} \subseteq [-1,0] \; \textbf{\textup{og}}\; \bigcap_{n=1}^{\infty }A_{n}\supseteq [-1,0]](https://media.studieportalen.dk/images/equations/K6U_RX7zpRGxcu6WnvZ5oA==.gif)