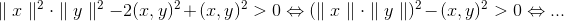Matematik
indre produkt
Hej,
Jeg har lidt problemer med vedhæftede fil.
<z,y> = <x ,rx> = r<x,x> = r IIxII^2 = I x I * I y I
Hvordan kan det passe at det indre pordukt <x,y> = I x I * I y I ? vil gerne se hele udledningen fra start til slut.
Svar #1
27. oktober 2016 af Eksperimentalfysikeren
I det, du har vedhæftet har du to tilfælde.
I det første er x og y lineært afhængige, og så gælder der at der findes et r, så y = rx. Det er det, der er omtalt i de to første linier. Her er så også udledt det, du spørger om i linie 2: <x,y> = <x,rx> = r<x,x> = r|x|2 = r|x|*|x| = |x|*|rx| = |x|*|y|. (Jeg har tilføjet et par trin.)
Jeg tror, du bliver forvirret over, at r bruges på to forskellige måder i de to tilfælde, så jeg vil benytte q i det følgende.
I det andet tilfælde er x og y lineært uafhængige. Det vil sige, at qx≠y for alle q∈R.
0 < <x+ry,x+qy> = |x|2 + 2q<x,y> + q2|y|2. ( = A, for nemheds skyld)
Så trækker vi en kanin op af hatten (Der er i forvejen en, der har regnet på tingene og fundet den bedst egnede kanin): q = -<x,y>/|y|2:
A = |x|2 - 2<x,y>/|y|2<x,y> + (-<x,y>/|y|2)2|y|2
= |x|2 -2<x,y>2/|y|2 + <x,y>2/|y|2
= |x|2 - <x,y>2/|y|2
Heraf:
<x,y>2 /|y|2 < |x|2, som ganges på beggesider af ulighedstegnet med |y|2:
<x,y>2 < |x|2 |y|2
Svar #2
27. oktober 2016 af bokaj123
Ja det er korrekt der er den trivielle løsning hvor de er lineært afhængige, men forstår ikke helt denne udledning. Vi har 2 vektorer x=(x1,x2,x3)' og y=(y1,y2,y3)'. hvorfor er <x,y> = r*<x,x> ....... = normen x * normen y? vi ved at y=r*x da de er lineært afhængige. det jeg i først omgang spørger til er det regnetekniske med indreprodukter. Hvis du kunne komme med et eksempel ville det måske hjælpe :)
<x,y> = <x,rx> = r<x,x> = r*|x|2 = r|x|*|x| = |x|*|rx| = |x|*|y|
Svar #3
27. oktober 2016 af AMelev
Det følgende er baseret på, at notationen <a,b> betyder skalarproduktet (jeg er ikke tidligere stødt på den notation).
#2<x,y> = <x,rx> = r<x,x> = r*|x|2 = r|x|*|x| = |x|*|rx| = |x|*|y|
Lineært afhængige: Jeg kan ikke helt lide den. Hvis r < 0, er skalarproduktet negativt, men produktet af normerne er positivt. Generelt gælder, at
1) ||x||2 = <x,x> og
2) ||r·x|| = |r|·||x||,
men i det uploadede er der ikke numerisk tegn om r, så lighedstegnet gælder kun, når r er positiv. Der skulle have stået: |<x,y>| =... |r| · ||x|| = |...=||x|| · ||y|| (ved lineært uafhængige er der også numerisktegn om skalarproduktet).
Lineært uafhængige: En lidt anden måde end #1
Da x + r·y ≠ 0, er længden af den positiv. Jeg bruger alm. () i stedet for de "vinklede" her, da det ellers kolliderer med "større end"-tegnet
||x + r·y|| > 0 ⇔ (iflg. 1) (x + r·y,x + r·y) > 0 ⇔ ||x||2 +2r·(x,y) + r2·||y||2 >0 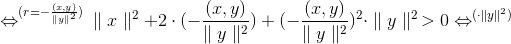
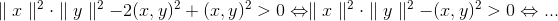
Svar #4
27. oktober 2016 af AMelev
Supplerende til #3
3) (a,t·b) = (t·a,b) = t·(a,b), hvor t ∈ R (tallet kan "sættes uden for skalarproduktet"
ad # 1 Måske er det lettere at "fange kaninen" her:
#3Lineært uafhængige:
||x + r·y|| > 0 ⇔ (iflg. 1) (x + r·y,x + r·y) > 0 ⇔ ||x||2 +2r·(x,y) + r2·||y||2 >0(Vi vil gerne have noget med ||x|| · ||y||, så vi ganger med ||y||2 )
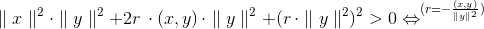
(Vi vil gerne af med ||y||2 og til gengæld gerne have noget med (x,y) i de to sidste led for at nærme os formlen, der skal vises. r skal altså hedde noget med (x,y)/||y||2. For at få det til helt at passe skal der et minus på.)
4). Hvis vektorerne x og y er i 2D eller 3D, kan sætningen bevises meget lettere:
Vi ved, at |(x,y)| = ||x|| · ||y|| · |cos(v)|, hvor v er vinklen mellem x og y. Da 0 ≤ cos(v)| ≤ 1 gælder så, at
|(x,y)| = ||x|| · ||y|| · |cos(v)| ≤ ||x|| · ||y||.
Svar #5
27. oktober 2016 af VandalS
Nu er udregningerne blevet gennemgået af flere omgange, men jeg vil gerne bidrage med lidt ekstra baggrundsviden.
Uligheden
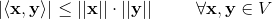
er en udgave af Cauchy-Schwarz ulighed og gælder i alle vektorrum V der er udstyret med et indre produkt 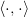 og den dertil tilhørende kanoniske norm
og den dertil tilhørende kanoniske norm 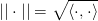 . Som du ser i din opgave gælder der lighed hvis og kun hvis de to vektorer
. Som du ser i din opgave gælder der lighed hvis og kun hvis de to vektorer 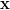 og
og 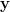 er lineært afhængige. Hvis du vil vide mere er der masser af information at hente om emnet, både på nettet og i bøger om f.eks. Hilbertrum eller reel analyse.
er lineært afhængige. Hvis du vil vide mere er der masser af information at hente om emnet, både på nettet og i bøger om f.eks. Hilbertrum eller reel analyse.
Svar #6
27. oktober 2016 af Eksperimentalfysikeren
#2 Jeg vil forsøge med vektorerne skrevet ud med koordinater. Det er nemmest af skrive på matrixform, så
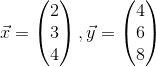
Det er rigtigt, at der er et problem med negative værdier af r, men det ignorerer jeg her. Det kan repareres, som gjort i andre svar. Mit valg af koordinater giver r = 2.
Det simple tilfælde skrives så:
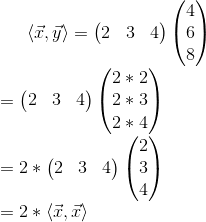
Jeg vil foreslå, at du selv prøver med den anden mulighed
#3: En bemærkning om notationen <x,y>. Der er flere forskellige notationer for skalarprodukt. Den viste er én af dem. I kvantemekanikken benytter man formen <x|y>, som kan udvides til f.eks. <x|A|y>, som er skalarproduktet mellem x-vektor og den med A transformerede y-vektor. Det engelske ord for <> er bracket. Det har givet anledning til, at man kalder <x| for en bra-vektor og |y> en ket-vektor og notationen for bra-ket-notation. I matrixform er en bra-vektor en rækkevektor (som det er vist ovenfor) og |y> en søjlevektor.
Svar #7
28. oktober 2016 af bokaj123
mange tak for de gode svar, der er lige en sidste ting
<x,x> = r* II x II2
nogen der kan forklare hvorfor det gælder? hvorfor er det indre produkt med sig selv = r * længden af x ^2
Svar #8
28. oktober 2016 af Eksperimentalfysikeren
<x,x> = r* II x II2 er ikke korrekt. Derimod <x,x> = II x II2 .
Skriv et svar til: indre produkt
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.