Matematik
Pseudoinverse Bevis.
Hej Derude.
Jeg har en opgave, der er rimeligt svært, især for mig.
Min bogen hjælper ikke med beviset, og derfor har brug for hjælp.
Vil nogen hjælpe med denne svær opgave. Det vil være hjælpsome, hvis nogen kan finde beviset, som en "Lecture Note"
.
Opgaven lyder som:
Bevis at pseudoinversen er en diskontinuert funktion af en matrix.
Hint: Beregn pseudoinverse af matricen.
 .
.
Nogen forslog, at man kan bruge normen til beviset, men det er ikke ret klar til mig.
Jeg håber, at nogen derude, kan finde en lecture note, eller vil hjælpe med opgaven.
På forhånd tak
Svar #1
28. oktober 2016 af Therk
Har du prøvet at beregne pseudoinversen, som hintet foreslår? Hvad får du? Og er den så kontinuert i epsilon?

Må jeg spørge af nysgerrighed: Dine spørgsmål rækker ret vidt! Hvad hedder det kursus du pt. tager og hvad studerer du? :)
Svar #2
29. oktober 2016 af Rossa
Jeg vil ikke skrive hvad jeg læser for mange grunde.
Dette kursus hedder Numeriske Analysis, og linket er: http://kurser.ku.dk/course/NMAA09005U
Jeg har lige læst idag om dette emne, og nu forstår jeg en lille smule mere end i går.
Definition i min bog er:
An arbitrary complex [m \times n] matrix A can be factored as:
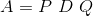
where P is ![[m \times m]](https://media.studieportalen.dk/images/equations/ZfX6JhwUbds4a3PSuJAdWQ==.gif) unitary matrix, D is an
unitary matrix, D is an 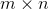 diagonal matrix and Q is an
diagonal matrix and Q is an 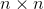 unittary matrix.
unittary matrix.
Her har vi:
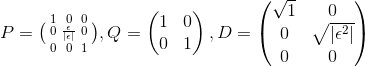
Pseudoinverse er defineret, og regnet dermed:
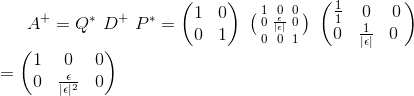 ,
,
Her kan man se, at hvis 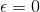 , så er måtte pseudoinversen være diskontinuert, eller ikke defineret.
, så er måtte pseudoinversen være diskontinuert, eller ikke defineret.
Måske er der mere end det, da nogle forslog, at bruge normen til at bevise opgaven.
Jeg håber, at du vil forslå noget mere.
Jeg glæder mig til at høre fra dig
Svar #3
31. oktober 2016 af Therk
Uha, glimrende fag!

Hvis du gerne vil vise det med en norm, tag da fx maks-normen af din pseudo-inverse.
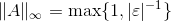
Lad epsilon gå mod nul. Hvad giver det?
Sammenlign med maks-normen af matricen for epsilon lig nul:
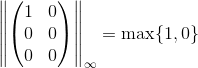
Konkludér at en funktion, der tager den pseudoinverse ikke kan være kontinuert på hele domænet.
Svar #4
31. oktober 2016 af Rossa
Nu forstår jeg opgaven som:
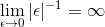 .
.
Det ville betyde, at pseudoinversen har en 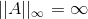 .
.
Og uendelige er ikke en konstat værdi, heller en værdi der vokser ukontrolleret.
Derfor kan man konkludere, at funktion der tager den pseudoinverse ikke kan være kontinuert på hele domænet, da 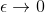 så
så 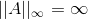 .
.
Mens epsilon er nul på matricen A, så er normen på A 1.
Er der også en anden metode.
Tak for hjælpen
Skriv et svar til: Pseudoinverse Bevis.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


