Matematik
Andenordenspolynomier og fitting
Hej, jeg prøver lige at starte en ny tråd op i dag om det samme emne som igår. Lad os sige at jeg har følgende to andenordenspolynomier y = -2,5x2+30x og y = -2,9x2+34,8x, hvordan finder jeg så den helt rigtige parameterfremstilling af x(t) således at jeg ved indsættelse af parameterfremstillingen for x(t) i den første andenordenspolynomie har den sidste andenordenspolynomie.
Håber at dette er til at forstå
Svar #1
11. januar 2017 af peter lind
Det hedder et 2. gradspolynomium
Du kan ikke indsætte en parameter så du får det andet polynomium
Svar #2
11. januar 2017 af Yipikaye
Hvis jeg ikke kan indsætte en parameter så jeg får det andet polynomium, kan jeg så i det mindste bruge det andet polynomium som et pejlemærke at fitte efter?
Svar #3
11. januar 2017 af peter lind
Nej. Men jeg har muligvis misforstået spørgsmålet nemlig hvis du mener om der findes en transformation, så du får det andet polynomium. Hvis det er det du mener kan du foretage transformationen x = a*t+b. sæt det ind i det første polynomium så du et nyt polynomium hvor koefficienterne skal stemme overens. senere kan du så omdøbe t til x
Svar #4
11. januar 2017 af Yipikaye
Hej igen og tak for svar. Jeg arbejder fortsat med emnet om paramerfremstilling, og det er i den forbindelse at jeg stiller spørgsmålet om hvorvidt man kan bruge det andet polynomium som et pejlemærke til fitting a curve.
Lad os sige at vi har følgende:
funktion nr 1. y = -2,5x2+30x.
Derudover så har vi nogle x og y-værdier. Disse x og y-værdier udtrykkes ved hjælp af en parameter (t) dvs. x(t) og y(t). Hvorefter parameteren (t) elimineres. Dermed haves det andet polynomium y = -2,9x2+34,8x.
Til sidst laves en parameterfremstilling af funktion nr. 1 y = -2,5x2+30x, hvor x udtrykkes ved parameteren (t), således at man ender med at have det andet polynomium nemlig y = -2,9x2+34,8x.
I må gerne give mig en be- eller afkræftelse på om man kan dette.
Svar #5
12. januar 2017 af Therk
Jeg forstår stadig ikke dit spørgsmål. Skal det forstås som at du ønsker at finde a i parameterfremstillingen
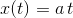
således følgende transformation er sand? I så fald, indsæt x(t) = at og isolér a
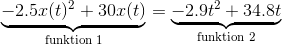
Vælg da fx (regn selv efter)
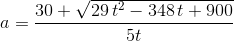

Skal vi være pedantiske, så er y = -2,9x2+34,8x en ligning og ikke et polynomie. Normalt er det okay ikke at skelne mellem de to, når det er underforstået hvad der menes. I dit tilfælde, hvor du bruger y til to forskellige udtryk er det ikke klart hvad du mener. Jeg har, herover, formodet at du mener at y implicit er afhængig af x i begge tilfælde og at det er to forskellige funktioner, udtrykt med det samme bogstav. For at undgå uklarhed, benyt to forskellige venstresider;
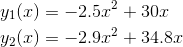
Svar #6
12. januar 2017 af Yipikaye
Hej Therk. Du har forstået hvad jeg mener, men jeg har stadig to spørgsmål. Spørgsmål 1) Jeg har ikke helt forstået hvordan du finder a ud fra ovenforstående formel. Spørgsmål 2) Kan man i det hele taget stille tingene op på den måde som jeg gør. Det jeg gør er at jeg sige at jeg har en objektiv funktion nemlig y = -2,5x2+30x, som jeg ønsker at fremstille ved hjælp af en parameter således at jeg ender med at have en funktion som svarer til de værdier som afstedkommer funktionen y = -2,9x2+34,8x.
Svar #7
12. januar 2017 af peter lind
I almindelighed kan du ikke. Et andetgradspolynomium er defineret ved 3 konstanter nemlig som y =a*x2+b*x+c Den eneste mde hor du kan få et andet 2,grads polynomiumud af der er ved at foretage en linær transformation x=d*t+e. Sådan en lineær transfomation har kun 2 parametre og kan derfor ikke give en vilkårlig andet polynomium
Svar #8
12. januar 2017 af Yipikaye
Men så er jeg næsten tilbage hvor jeg startede. Jeg er fortsat et stort spørgsmåltegn omkring dette emne. Jeg vil lige høre om der er nogen som kan anbefale noget litteratur om parametersering/parameterfremstilling.
Svar #10
13. januar 2017 af Yipikaye
Der er en række matematiske emner som jeg ønsker at forstå fuldt ud herunder projektion, planintegral, kurveintegral og ikke mindst parameterisering.
Svar #11
13. januar 2017 af fosfor
Hvis du har to andengradspolynomier:
f(t) = a·t2 + b·t + c
g(t) = A·t2 + B·t + C
så kan du opnå det sidste andengradpolynomium ved at sammensætte det første andenpolynomium med x(t) ved mindre både a = 0 og b = 0. Når f(x(t)) sættes lig g(t) fås bare en simpel ligning mht. x(t):
f(x(t)) = g(t)
a·x(t)2 + b·x(t) + c = A·t2 + B·t + C
Hvis a ≠ 0 har du to muligheder for et givet t, nemlig:
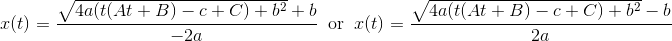
Hvis a = 0 er der kun en løsning, da ligningen bliver en førstegradsligning:
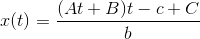
Hvis a = 0 og b = 0, bliver ligningen en nultegradsligning som ikke har en løsning.
Dvs i dit tilfælde med a = -2.5, b = 30, A = -2.9, og B = 34,8 er der for alle t to løsninger, så du kan ikke snakke om præcis den x(t) der gør det rigtige. Der er ikke en unik løsning.
Svar #12
13. januar 2017 af peter lind
Hvis a ≠ 0 har du to muligheder for et givet t, nemlig
Det skal altså gælde for alle t
Skriv et svar til: Andenordenspolynomier og fitting
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

