Matematik

Areal - funktion

11. januar 2017 af ForvirretBarn (Slettet) - Niveau: B-niveau

Hej med jer!

Jeg sidder fuldstændig fast i denne opgave. Jeg må gerne bruge N spire til hjælp, så håber i kan hjælpe! Den skal afleveres i morgen, så håber på hurtigt svar - tak på forhånd!

Vedhæftet fil: Skærmbillede 2017-01-11 kl. 20.23.19.png

Brugbart svar (0)

Svar #1
11. januar 2017 af mathon

Brugbart svar (0)

Svar #2
11. januar 2017 af mathon

$A_{samlet}=\int_{-1}^{2}(f(x)+7)\, \mathrm{d}x+\int_{2}^{4}(-7-f(x))\, \mathrm{d}x$

Svar #3
11. januar 2017 af ForvirretBarn (Slettet)

Tusind tak! Må jeg spørge hvor du får tallene fra? Sikkert et dumt spørgsmål, men så lærer jeg også lidt, haha :)
Men mange tak!

Brugbart svar (0)

Svar #4
11. januar 2017 af mathon

Skæringspunkternes førstekoordinater er integrationsgrænser.

Skæring kræver:
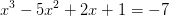
x^3-5x^2+2x+1=-7

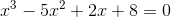
x^3-5x^2+2x+8=0

Hvis
differencen mellem koefficienterne til de de ulige potenser af x og koefficienterne til de lige potenser
af x er lig med 0, er x = -1 en rod.

her
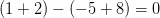(1+2)-(-5+8)=0 hvorfor -1 er en rod og dermed (x-(-1)) = (x+1) en divisor.

Faktorisering giver:
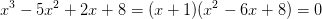
x^3-5x^2+2x+8=(x+1)(x^2-6x+8)=0

    og
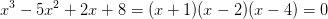
                                x^3-5x^2+2x+8=(x+1)(x-2)(x-4)=0
    dvs
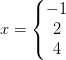
   $x=\left\{\begin{matrix} -1\\2 \\ 4 \end{matrix}\right.$

Skriv et svar til: Areal - funktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.