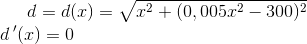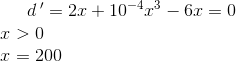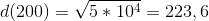Matematik

afstand mellem punkt of andengradsfunktion

16. februar 2017 af Jakobnil (Slettet) - Niveau: A-niveau

Hvordan finder jeg frem til den korste afstand imellem punktet p og funktionen 0.005*x^2+200

Vedhæftet fil: vej.JPG

Brugbart svar (0)

Svar #1
16. februar 2017 af janhaa

P=(0, 500) og (x, f(x))

korteste avstand er således:

$d = d(x) = \sqrt{x^2 + (0,005x^2-300)^2} \\d\, ' (x) = 0$

$d\, ' = 2x +10^{-4}x^3-6x=0\\ x > 0\\ x =200$

Brugbart svar (0)

Svar #2
16. februar 2017 af peter lind

Brugbart svar (0)

Svar #3
16. februar 2017 af peter lind

Brug afstandsformlen for kvadratet på afstanden mellem to punkter. Da y er en funktion af x, kan du erstatte y med funktionsudtrykket. Resultatet bliver en funktion af x

Svar #4
16. februar 2017 af Jakobnil (Slettet)

Jeg har tjekket facit til opgave og umiddelbart skulle minimumsafstanden være 223 meter

men jeg ved bare ikke hvordan man kommer frem til det

Brugbart svar (0)

Svar #5
16. februar 2017 af peter lind

Du differentiere d² og sætter resultatet = 0. Det x der giver minimum findes blandt løsningerne

Brugbart svar (0)

Svar #6
16. februar 2017 af janhaa

#4
Jeg har tjekket facit til opgave og umiddelbart skulle minimumsafstanden være 223 meter

men jeg ved bare ikke hvordan man kommer frem til det

d(200) = 223,6 m

Brugbart svar (1)

Svar #7
16. februar 2017 af janhaa

$d(200)=\sqrt{5*10^4}=223,6$

Svar #8
17. februar 2017 af Jakobnil (Slettet)

tusind tak det var en stor hjælp :D

Skriv et svar til: afstand mellem punkt of andengradsfunktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.