Matematik
Opgave analyse omkring grænseopførslen
Opgaven lyder:
Vis at:
En der kan hjælpe mig med denne?
Hovedsætning 2A er:
Svar #1
17. februar 2017 af VandalS
Nu specificerer du ikke, hvilke midler du må gøre brug af, men her er i hvert fald en måde at angribe det på:
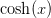er en kontinuert funktion voksende på intervallet 
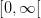med den egenskab, at 
.
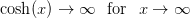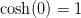, så 1 er med i værdimængden og er den mindste værdi, idet funktionen er voksende på intervallet.
Lad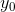 
være et vilkårligt reelt tal større end 1.
Da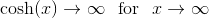 
eksisterer der et 
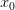sådan at 
.
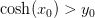Per Hovedsætning 2A konkluderer vi, at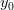 
er et element i værdimængden ![\cosh([0,x_0])](https://media.studieportalen.dk/images/equations/ZjbX4_GEbwJmDC9VQbUvWQ==.gif)
og derfor også et element i det større sæt 
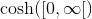. Da 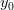er et vilkårligt reelt tal større end 1 konkluderer vi desuden, at der ikke kan findes nogen øvre grænse for værdimængden.
Tilsammen viser det, at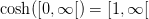 
som ønsket.
Skriv et svar til: Opgave analyse omkring grænseopførslen
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.