Matematik
Etabler ulighederne i analyse 0
Jeg skal etablere ulighederne:

Er der nogen der kan give råd og hjælp til denne opgave? Eksemplet i bogen er:

Svar #1
17. februar 2017 af AskTheAfghan
Det sidste billede viser, at |ex - 1| < 3|x| for x < 1/2. Du kan godt bruge denne ulighed for |x| < 1/2. Du har 2sinh(x) = ex - e-x = (ex - 1) - (e-x - 1). Benyt nu trekantuligheden, og den ulighed du skal bruge.
Svar #2
17. februar 2017 af Sluntegøj
Men hvordan får du:
2sinh(x)=ex-e-x=(ex-1)-(e-x-1)
Og det er trekantsuligheden jeg kun skal bruge, ikke sandt?
Svar #3
18. februar 2017 af Stats
For |cosh x - 1|
Vil det så være:
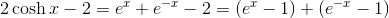
For jeg kan simpelthen ikke etablere en ulighed (e-x - 1) ≤ 3|x|
Mvh Dennis Svensson
Svar #4
18. februar 2017 af Stats
Jeg gør ligesom med |sinh x| bare med omvendt fortegn.
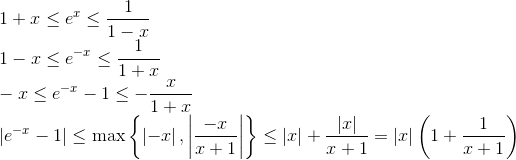
Mvh Dennis Svensson
Svar #5
18. februar 2017 af Stats
Hov... Vent lidt.. Den maksimale værdi er også 3... Jeg skulle bare have undersøgt for -0.5 :)
Mvh Dennis Svensson
Svar #6
18. februar 2017 af Sluntegøj
Jeg kan simpelthen ikke finde hoved og hale i det, har du formået at se fidusen i den, #5?
Svar #7
18. februar 2017 af AskTheAfghan
#2 Se på definitionen for sinh. Her er |(ex - 1) - (e-x - 1)| ≤ |ex - 1| + |e-x - 1| for alle reelle x. Dette kommer fra trekantuligheden. Benyt nu uligheden fra billede nr 2. Husk nu, at billedet nr. 2 gælder for alle x i (-∞,1/2), så burde den også gælde for alle x i (-1/2,1/2), idet (-1/2, 1/2) ⊆ (-∞,1/2). Specielt er |e-x - 1| ≤ 3|-x| = 3|x| for alle |-x| = |x| < 1/2.
#3-5 Korrekt. Nu er 2|cosh(x) - 1| ≤ |ex - 1| + |e-x - 1| for alle x. Kig på den ovenstående tekst.
Svar #8
18. februar 2017 af Oatmeal (Slettet)
#7 Hvordan får du |(ex - 1) - (e-x- 1)| ≤ |ex - 1| + |e-x - 1| af trekantsuligheden? Hvordan bliver - på venstre side af ulighedstegnet til + på højre side?
Skriv et svar til: Etabler ulighederne i analyse 0
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








