Matematik
Overfladeareal af pyramide med kvadratisk bund
Hej. Jeg har lidt svært ved denne opgave, som lyder således:
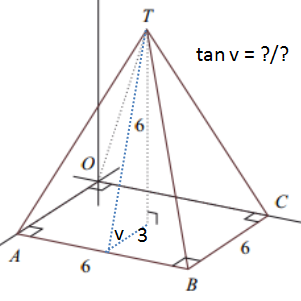
Billedet ovenfor viser en flødebolle, der har form som en pyramide med kvadratisk bund. Toppunktet af pyramiden ligger på en linje, der står vinkelret på diagonalernes skæringspunkt i bunden. Den kvadratiske bund har sidelængden 6 cm, og afstanden fra toppunktet til bunden er 6 cm.
Benyt modellen til at bestemme det samlede overfladeareal af flødebollen inklusiv bunden.
Hvilken formel er det helt præcis jeg skal bruge?
Svar #1
17. februar 2017 af Eksperimentalfysikeren
Du skal benytte Pythagras til at finde højden i siderne.
Svar #2
17. februar 2017 af biotek222 (Slettet)
Men er alle sidelængderne ikke bare de 6cm?
Fordi så jeg en formel som lyder: overfladearealet af pyramiden=arealet af grundlinjen*siderne*1/2*højden af trekanten*g
Kan det passe at det er den jeg skal bruge? Og hvis det er, hvordan finder jeg så grundlinjen og arealet af grundlinjen?
Svar #3
17. februar 2017 af biotek222 (Slettet)
Her er et billede af opgaven samt figur
Svar #4
17. februar 2017 af StoreNord
Grundfladens sider er 6, og pyramidens højde er 6.
#1 snakker om hver skrå trekantet side som læner sig skråt ind mod pyramidens top.
I disse trekanter har du en grundlinje på 6, men du mangler en (skrå) højde.
Svar #6
17. februar 2017 af biotek222 (Slettet)
# 4 Okay det forstår jeg godt, så kan jeg vel projicerer T ned på linjen. Men hvordan finder jeg koordinatsættet til T og C, hedder det bare (6,0,0) og (6,0,0) eller hvad? For der står jo kun 6 til dem begge
Svar #8
17. februar 2017 af StoreNord
#6
C ligger i (0,6,0) og T ligger i (3,3,6) (håber du ved hvad du skal bruge det til.)
Svar #9
17. februar 2017 af SuneChr
# 6 Nej, la' vær' med at lade dig distrahere af koordinater. De er ikke nødvendige for dette simple legeme.
Benyt almindelig geometri som foreslået.
Svar #10
17. februar 2017 af biotek222 (Slettet)
Det gør jeg, men der er et eller andet der går galt i mine udregninger, fordi det kommer til at give 0
Svar #11
17. februar 2017 af Eksperimentalfysikeren
Her har du jo netop brugt koordinater. Jeg kan ikke se, hvad du forsøger at gøre. Teksten er næsten ulæselig og der mangler forklaringer.
Det bedste, du kan gøre, er at glemme alt om koordinater og regne med ren geometri.
Se på et snit gennem puramidens toppunkt og gennem midtpunkterne af to modstående sider. Det giver en ligebenet trekant, hvor højden er 6 og grundlinien er 6. Brug Pythagoras til at regne længden af de to skrå sider ud. Du kan desuden finde vinklen mellem den skrå side og grundfladen, for det er det samme som vinklen ved grundlinien i trekanten.
Disse to sider i trekanten er højderne i de to trekanter, der danner to af siderne i pyramiden. Når du har højden i sidetrekanten, kan du finde dens areal, for du har grundlinien, der er 6.
Derefter ganger du med 4, fordi der er 4 sider i pyramiden, og lægger grundfladens areal til
Skriv et svar til: Overfladeareal af pyramide med kvadratisk bund
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.