Matematik
Bur med net over
Hvis man skal lave et bur med net over det, og du har 5m2 net i det hele, hvor lange skal siderne af burret så være, hvis man skal have det maximale rumfang af burret?
Gulvet af burret skal ikke dækkes af net, det er kun de fem ydderste sidder.
Tak på forhånd
- Magnus
Svar #1
28. februar 2017 af PeterValberg
Må du klippe nettet i mindre stykker ?
I så fald ville jeg klippe de 5 m2 net op i fem
kvadratiske stykker, hver på 1 m2, dermed
kan du lave en terning på 1 m3, hvor der er
net på de fem sider, - det må være det optimale.
Svar #3
28. februar 2017 af hesch (Slettet)
#1: Nej, så let slipper du ikke, for det er ikke en (symmetrisk) kubus, der er tale om: Bunden har ikke net.
Beregner man arealforbrug af net findes: ( B=bredde, L=længde, H=højde )
A = 2BH + 2LH + 1BL = 5
I denne ligning er B og L fuldstændig symmetriske, og man kan derfor substituere: B = L = S , S=sidelængde.
Således kan ligningen formuleres: S2 + 4HS - 5 = 0 , og maximere volumen: V = HS2.
Nu er jeg så ikke så skarp til matematik, og har derfor bekvemt valgt at foretage optimeringen numerisk:
- Varier H fra 0,01mm til 10,00000 m ( sandsynlig øvre grænseværdi for højden )
- Find S ved løsning af 2. grads ligningen.
- Beregn HS2 = Volumen
- Gem største volumen sammen med tilhørende S og H
Efter 2 sek. beregning finder min PC:
B = L = 1,29099 m , H = 0,64550 m
Volumen = 1 m3 1,07583 m3 ( min fremhævning ).
Svar #4
28. februar 2017 af SuneChr
De numeriske beregninger i # 3 stemmer godt overens med de analytisk udledede beregninger, som dog
ikke er pensum på 9. klassetrin, men her bringes de alligevel.
Har valgt at sætte
længden = x
bredden = y
højden = z
Det fører til
2xz + 2yz + xy = 5 ⇒ 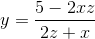 ∧ V = xyz ⇒
∧ V = xyz ⇒ 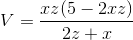
Ved partieldifferentiation af V og sætte lig 0 , har vi to ligninger i x og z :
4xz + x2 - 5 = 0 ∧ - 4 xz - 4z2 + 5 = 0 ⇒
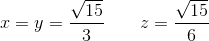 som giver et maksimalt rumfang på
som giver et maksimalt rumfang på 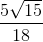
Svar #5
01. marts 2017 af SuneChr
Generelt kan udledes formlen for sammenhængen imellem overfladen af en kasse, minus bunden, og dens
maksimale rumfang.
Man har
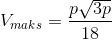 hvor p er overfladen af kassen, minus bunden.
hvor p er overfladen af kassen, minus bunden.
Længden = bredden = 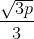 og højden er
og højden er 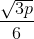
Man ser da, at højden altid er halvdelen af længden og dermed også halvdelen af bredden.
Svar #6
01. marts 2017 af PeterValberg
Hvis spørger angiver niveauet korrekt (9. klasse), så synes jeg,
at det er en meget svær opgave, læreren har givet sine elever.
Jeg tvivler på, at partieldifferentiation (som anvendt i #4 af SuneChr) er pensum i folkeskolen ;)
Skriv et svar til: Bur med net over
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




