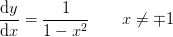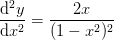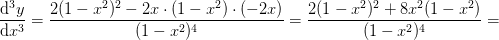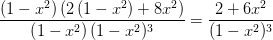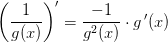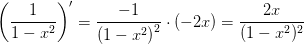Matematik

Højere-ordens afledte

20. marts 2017 af JohnDoe1990 - Niveau: Universitet/Videregående

Jeg skal vise at nedenstående afledte er givet i intervallet (-1,1) ved:

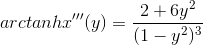
$arctanhx ''' (y) = \frac{2+6y^2}{(1-y^2)^3}$

og jeg har udregnet i forvejen at

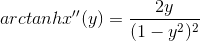
$arctanhx '' (y) = \frac{2y}{(1-y^2)^2}$

...men jeg kan ikke få det ønskede udtryk. Jeg får i stedet det forkerte fortegn i tælleren:

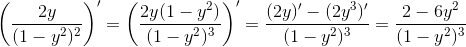
$\left ( \frac{2y}{(1-y^2)^2} \right )' = \left ( \frac{2y(1-y^2)}{(1-y^2)^3} \right )' = \frac{(2y)'-(2y^3)'}{(1-y^2)^3} = \frac{2-6y^2}{(1-y^2)^3}$

Hvad er det som jeg gør forkert? Håber I kan hjælpe.

Mvh.

Brugbart svar (0)

Svar #1
20. marts 2017 af mathon

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1}{1-x^2}\; \; \; \; \; \; \; x\neq \mp 1$

$\frac{\mathrm{d}^2 y}{\mathrm{d} x^2}=\frac{2x}{(1-x^2)^2}$

$\frac{\mathrm{d}^3 y}{\mathrm{d} x^3}=\frac{2(1-x^2)^2-2x\cdot (1-x^2)\cdot (-2x)}{(1-x^2)^4}=\frac{2(1-x^2)^2+8x^2(1-x^2)}{(1-x^2)^4}=$

$\frac{\left ( 1-x^2 \right )(2\left (1-x^2 \right )+8x^2)}{\left ( 1-x^2\right )(1-x^2)^3}=\frac{2+6x^2}{(1-x^2)^3}$

Svar #2
20. marts 2017 af JohnDoe1990

Hej Mathon. Mange tak for din hjælp. :-) Jeg er ikke helt med på den første lighed:

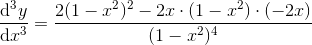
$\frac{\mathrm{d^3} y}{\mathrm{d} x^3} = \frac{2(1-x^2)^2-2x \cdot (1-x^2) \cdot (-2x)}{(1-x^2)^4}$

Jeg kan forstå at du forlænger den anden afledte ved at multiplicere tæller og nævner med (1-x^2)^2. Er dette korrekt forstået? Men kan alligevel ikke se, hvordan du kommer frem til første lighed. Er ret frustreret over, at jeg ikke kan finde ud af det. Jeg er dog med på det resterende.

Brugbart svar (0)

Svar #3
20. marts 2017 af mathon

Jeg forlænger ikke,
men benytter
$\left ( \frac{1}{g(x)} \right ){}'=\frac{-1}{g^2(x)}\cdot g{\, }'(x)$

som aktuelt
giver:
$\left ( \frac{1}{1-x^2} \right ){}'=\frac{-1}{\left (1-x^2 \right )^2}\cdot(-2x)=\frac{2x}{(1-x^2)^2}$

Svar #4
20. marts 2017 af JohnDoe1990

Nu forstår jeg det. Tak for hjælpen.

Skriv et svar til: Højere-ordens afledte

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.