Matematik

Uniform konvergens

11. maj 2017 af Stats - Niveau: Universitet/Videregående

$\\ \textup{Lad }n\in\mathbb{N} \textup{ og definer }h_n:[0,\infty[\to\mathbb{R} \textup{ ved}\\ \\ {\color{white} .}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h_{n+1}(x)=\sqrt{h_{n}}\textup{ med }h_1=x\\ \\ \textup{Lad }b>a>0.\textup{ Vis at }\{h_n\}_{n\in\mathbb{N}} \textup{ konvergere uniformt p\aa}\ [a,b] \textup{ og vis derefter at:}\\ \\ {\color{white} .}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall\varepsilon>0,\exists N\in\mathbb{N},\forall n,m>N:\ d_A(h_n,h_m)\leq \varepsilon,\\ \\ \textup{dvs, vis at }\{h_n\}_{n\in\mathbb{N}} \textup{ er en Cauchyf\o lge af funktioner p\aa }\ [a,b].$

Jeg viser at den konvergere uniformt:

$\\ \lim\limits_{n\to\infty}d_{[a,b]}(h,h_{n+1})=\lim\limits_{n\to\infty}\sup\{|h(x)-h_{n+1}(x)|:x\in[a,b]\}\\ =\lim\limits_{n\to\infty}\sup\left\{\left|1-x^{\left( \frac{1}{2}\right )^n}\right|:x\in[a,b]\right\}=\sup\left\{|1-x^0|:x\in[a,b]\right\}=0$

Det næste jeg skal vise - jeg aner ikke hvor jeg skal starte... Men jeg forsøger

$\\ \sup\left\{\left|x^{\left( \frac{1}{2}\right )^n} - x^{\left( \frac{1}{2}\right )^m}\right|:x\in[a,b]\right\}= \sup\left\{\left|x^{\left( \frac{1}{2}\right )^n} - 0 + 0 - x^{\left( \frac{1}{2}\right )^m}\right|:x\in[a,b]\right\}\\ \leq\sup\left\{\left|x^{\left( \frac{1}{2}\right )^n} - 0\right| + \left|0 - x^{\left( \frac{1}{2}\right )^m}\right|:x\in[a,b]\right\}$

Hmmm.... Aghr... Kan simpelthen ikke forstå det.. 8-|

Brugbart svar (1)

Svar #1
12. maj 2017 af Number42

Du kan vise at siden serien er konvergent så er x^{(1/2)^n} < epsilon for n > N og det gælder også for x^{(1/2)^m}

det gælder derfor også for differensen.

Svar #2
12. maj 2017 af Stats

Altså: Lad ε>0, så må jeg finde et N sådan at |x^{(1/2)^n} - x^{(1/2)^m}| < ε. Siden at {x_n} og {x_m} konvergere mod en grænsefunktion, findes der et N sådan at |1 - x^{(1/2)^m}| < ε/2 og et N sådan at |x^{(1/2)^n} - 1| < ε/2 for alle m ≥ N. Hvis n,m ≥ N, så er

|x^{(1/2)^n} - x^{(1/2)^m}| = |(x^{(1/2)^n} - 1) + (1 - x^{(1/2)^m})| ≤ |x^{(1/2)^n} - 1| + |1 - x^{(1/2)^m}| < ^ε/₂ + ^ε/₂ = ε.

Er det rigtigt? (jeg glemte at grænsefunktionen var 1.)

- - -

Mvh Dennis Svensson

Brugbart svar (1)

Svar #3
12. maj 2017 af Therk

Hint:

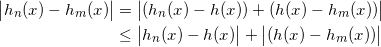
$\begin{align*}\bigl\lvert h_n(x)-h_m(x) \bigr\rvert&= \bigl\lvert (h_n(x)-h(x)) + (h(x) -h_m(x))\bigr\rvert \\&\leq \bigl\lvert h_n(x)-h(x)\bigr\rvert + \bigl\lvert(h(x) -h_m(x)) \bigr\rvert \end{align*}$

$\rule{7cm}{0.4pt}$

Har du vist at følgen konvergerer mod h(x) = 1 før her eller har du (kvalificeret) gættet det og vist det a posteriori med dit bevis for at konvergensen er uniform? Hvis du ikke har vist det tidligere, så synes jeg det er værd at bemærke i hvert fald.

Undgå at benytte limes-notation i dine beviser. Eksempelvis siger du at

$\lim\limits_{n\to\infty}d_{[a,b]}(h,h_{n+1})=\lim\limits_{n\to\infty}\sup\{|h(x)-h_{n+1}(x)|:x\in[a,b]\}$

men det du mener er at

$d_{[a,b]}(h,h_{n+1})=\sup\{|h(x)-h_{n+1}(x)|:x\in[a,b]\}$

På dette tidspunkt har du ikke fortalt læseren endnu at grænsen eksisterer - og i tilfælde af at grænsen ikke eksisterer, så er det øverste udtryk meningsløst. Hold dig i stedet til at slutte af med en konvergenspil, når det er det, du vil fortælle læseren at der sker.

Brugbart svar (1)

Svar #4
12. maj 2017 af Therk

Jeg kan se at jeg var lidt langsom til at skrive mit svar og du allerede har brugt hintet fra #3 i #2. :) Jeg håber du kan bruge min anden kommentar.

Ja, det ser fint ud i #2

Svar #5
12. maj 2017 af Stats

Tak. :)

Men i min bog bruger de definitionen:

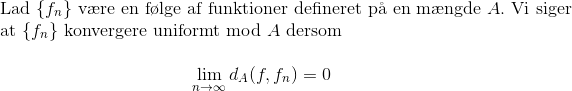
$\\ \textup{Lad }\{f_n\}\textup{ v\ae re en f\o lge af funktioner defineret p\aa\ en m\ae ngde }A.\textup{ Vi siger}\\ \textup{at }\{f_n\}\textup{ konvergere uniformt mod }A\textup{ dersom}\\ \\ {\color{white}......................................}\lim\limits_{n\to\infty}d_A(f,f_n)=0$

Og definitionen på afstanden var d_A(f,f_n) = sup{|f(x) - f_n(x)| : x∈A}

Årsag til at jeg anvendte lim tegnet, var fordi at jeg skulle vise at den var uniform konvergent i starten... :)

- - -

Mvh Dennis Svensson

Brugbart svar (1)

Svar #6
12. maj 2017 af Therk

Formelt er der ingen forskel, dvs.

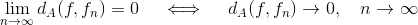
$\lim_{n\to\infty}d_A(f,f_n) = 0 \quad \iff \quad d_A(f,f_n)\to 0, \quad n\to \infty$

men i et bevis, hvor formler og ligninger fungerer som "normal tekst", der læses fra venstre til højre, så læses sidstnævnte bedre (før grænsen er etableret).

Du kan derfor gøre som herunder

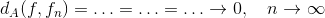$d_A(f,f_n) = \ldots = \ldots = \ldots \to 0, \quad n\to \infty$ ,

hvilket, for venstre-til-højre-læsere, giver det et bedre flow, og viser bedre dine argumenter.

Misforstå mig endelig ikke: Det er ikke forkert, det du gør, men gør det mindre åbenlyst hvad der sker.

Brugbart svar (1)

Svar #7
12. maj 2017 af AskTheAfghan

Den første del af opgaven har du pludselig rykket limes indenfor supremum for mængden J := {|h(x) - h_n+1(x)| : x ∈ [a, b]}. Må man det? Du har ikke vist, om supremum for J eksisterer. Start med at finde et dygtigt overtal for J (i så fald vil, idet J ≠ ∅, supreum for J findes), og så bestemmer man grænseværdien for overtallet. Jeg tror, det er nemmere at arbejde med opgaven ved brug af Dinis sætning.

Skriv et svar til: Uniform konvergens

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.