Matematik
Ln og Log
Hej Studieportalen
Jeg skal til eksamen her om et par dage i matematik b.
Jeg er meget i tvivl om hvornår jeg ´ bruger ln (den naturlige logaritme) og log(titalslogaritmen).
Jeg skal blandt andet bruge dem til at løse følgende opgaver:
1) 2,3*1,7^x = 19,2
Til denne opgave har jeg løst den ved hjælp af log, hvor jeg fik svaret til at være 3,999 omregnet til decimaler.
2) 5,9*0,8^x= 1,4*1,3^x
Til denne opgave brugte jeg ln, hvor jeg fik svaret til at blive 2,962.
Kan i bekræfte om det jeg er kommet frem til er korrekt :) Og forklarer hvorfor jeg i disse tilfælde skal bruge henholdvis log og ln, og komme med en redegørelse på logaritme reglerne.
Tak på forhånd!
Svar #2
12. juni 2017 af janhaa
ln(e) = 1
log(10) = 1
1)
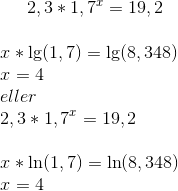
dvs samme hvem du bruker.
De har ulike grunntall (e og 10).
Svar #3
12. juni 2017 af PeterValberg
Dine resultater er korrekte.
Der er i denne sammenhæng ingen forskel på,
om du bruger ln eller log, idet:
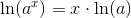
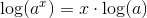
se i øvrigt denne tråd < LINK >
Svar #4
12. juni 2017 af SuneChr
I tiden, før de første lommeregnere kom på markedet, anvendte man, i skolen, logaritmen med grundtallet 10. Det har sine praktiske fordele. log (a·10n) = (log a) + n .
Til mere teoretiske overvejelser kom ln funktionen ind i billedet.
Enhver logaritmefunktion kan benyttes. De er alle indbyrdes proportionale.
1) 3,99903539...
2) 2,96283616...
Svar #5
12. juni 2017 af Eksperimentalfysikeren
Der er en del tilfælde, f.eks. de to, du har omtalt, hvor valget af logaritmefunktion er en smagssag.
Da man tidligere benyttede logaritmer til tekniske beregninger og navigation, var det 10-talslogaritmen, der blev benyttet, fordi man kunne nøjes med en logaritmetabel, der dækkede området 1,0000 til 9,999. Skulle man finde logaritmen til et tal udenfor dette område, dividrede man det med 10n og lagde n til tabelværdien, fordi log (a·10n) = (log a) + n, som nævnt i #4.
Skal man benytte antallet af cifre i et tal, skal man vælge den logaritme, der har samme grundtal som talsystemet. Er tallet skrevet i 10-talssystemet, er antallet af cifre ca. log10 af tallet. Er det skrevet i 2-talssystemet, er antallet af cifre ca. log2 af tallet. Det sidste benyttes til vurdering af regnehastigheder ved regning på meget store tal i computerteknikken.
Hvis man får en logaritme som resultat af en integration eller som løsning på en differentialligning, er det nemmest at arbejde med den naturlige logaritme.
Lysfølsomheen af film angives på flere forskellige måder. Den ene er DIN-skalaen, der er logaritmisk. Grundtallet er den tiende rod af 10. Derved svarer 10 trin på skalaen til en faktor 10 i følsomhed.
Svar #6
06. juli 2017 af mathon
opfølgning på #1
Logaritmefunktioner er proportionale, hvorfor det i beregninger, hvori der kun optræder
logaritmeforhold, ikke har nogen betydning, hvilken logaritme der anvendes.
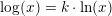
hvoraf:
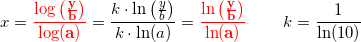
Svar #7
06. juli 2017 af SuneChr
Lidt sommerferie overvejelser når nu det er matematisk agurketid.
# 6
Der er tradition for, at betegne proportionalitetsfaktoren for log10 og ln for M
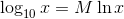
hvor M er lig med k i # 6 .
Jeg har som ikke tænkt nærmere over, hvad dette store M kommer af, men kan måske være forbogstavet for multiplikator eller multiplikand.
En anden ting er, - at hvorfor sætter man parentes om argumentet i log og trigonometriske funktioner, når argumentet kun består af en enkeltstående variabel? Det forstås, når argumentet er af flere led eller sammensat af faktorer, at det er indlysende at sætte en parentes. I lærebøger, formelsamlinger m.m. fra tidligere tider brugte man ikke denne parentes. Det ligger måske i, at man har almengjort afbildningssymbolet f (x) til også at gælde log og sin , når f (x) = log x og f (x) = sin x .
For funktionen f (x) = ex benyttes jo ikke f (x) = e(x) og endda heller ikke, selv om eksponenten er af flere led eller flere faktorer, hvilket i øvrigt heller ikke ville kunne mistolkes i dette tilfælde.
En tredje ting: Hvordan er "integrale" kommet ind som betegnelse for integral? Man ser det i nogle moderne forfatteres lærebøger, og mange brugere herinde skriver det også.
I den i øvrigt udmærkede formelsamling "Matematik 112" af Lars Pedersen benyttes integrale også.
Svar #8
06. juli 2017 af Eksperimentalfysikeren
Programmeringssprogene kan ikke finde ud af, hvad f.eks. sin x betyder. De har brug for parenteserne. Man kan godt designe compilerne, så de kan finde ud af det, men det er en hel del nemmere (i hvert fald for compilerkonstruktørerne) at vedtage, at man altid skal benytte parentes. Det giver så også den fordel, at det er nemmere at se, om sin x2 betyder (sin x)2 eller sin(x2). I gamle dage skrev man sin2 x, hvis kvadreringen skulle sidst: sin2 x +cos2 x = 1.
Skriv et svar til: Ln og Log
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

