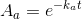Matematik

Løsning til differentialligning

25. juni 2017 af swampendk (Slettet) - Niveau: A-niveau

Hej

Er der nogen der ved hvordan man læser denne differentialeligning ( ift farmakokinetik, absrobtion/elimination):
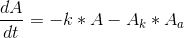
$\frac{dA}{dt} = -k*A-A_k*A_a$

Sådan at resultatet bliver til :

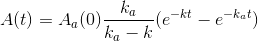
$A(t)=A_a(0) \frac{k_a}{k_a-k}(e^{-kt}-e^{-k_at})$

Kan simpelthen ikke gennemskue det. Har prøvet vha. seperation af variable, og har prøvet at bruge alle mulige DE solvers jeg kunne støve op på google, men desværre uden at finde noget brugbart.

Brugbart svar (0)

Svar #1
25. juni 2017 af peter lind

Hvad er A_k og A_a ? Da jeg ikke ved det så med forbehold. Brug panserformlen. y' + a(x)*y = f(x) har løsningen y = e-^A(x)∫e^A(x)*f(x)dx hvor A(x) er en stamfunktion til a(x)

Svar #2
25. juni 2017 af swampendk (Slettet)

Ja, det er lidt pinligt men jeg glemte at få det med der stod på linjen nedenunder

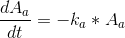
$\frac{dA_a}{dt}=-k_a*A_a$

Får Aa til A_0*exp(-k_a), men kan nu stadig ikke få det til at passe.

Brugbart svar (0)

Svar #3
25. juni 2017 af Number42

$A_a = e^{-k_a t}$

Det er en løsning man kender eller let gætter.

Svar #4
25. juni 2017 af swampendk (Slettet)

Ja, men forstår stadig ikke hvordan det bliver til det der står i A(t) i spørgsmålet :)

Brugbart svar (0)

Svar #5
25. juni 2017 af peter lind

Hvad er A_k ?

Svar #6
25. juni 2017 af swampendk (Slettet)

ahrg... A_k er selvfølgelig k_a - undskyld!

Brugbart svar (0)

Svar #7
26. juni 2017 af peter lind

Så får du differentialligningen dA_a/dt = -k_aA_a -k_a*A_a = -2*k_a*A_a.

Kan vi ikke få den rigtige differentialligning? Start helt forfra

Svar #8
26. juni 2017 af swampendk (Slettet)

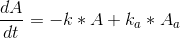
$\frac{dA}{dt}=-k*A+k_a*A_a$

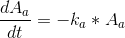
$\frac{dA_a}{dt}=-k_a*A_a$

Den oplyste løsning er følgende:

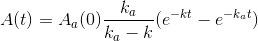
$A(t)=A_a(0)\frac{k_a}{k_a-k}(e^{-kt}-e^{-k_at})$

(undskyld forvirringen - det ovenstående er som det står i min beskrivelse )

Brugbart svar (0)

Svar #9
26. juni 2017 af peter lind

Nu er der igen forskel på indeks. Hvad er dem med indeks a og dem uden a

Svar #10
26. juni 2017 af swampendk (Slettet)

Med index, mener du så det der står i subscript?

I mine slides står der at: k er eliminationsraten [pr. time] og k_a er absorbtionsraten [pr. time]. A er mængde medicin i kroppen[mg], A_a er mængde medicin som endnu ikke er absorberet [mg].

Brugbart svar (0)

Svar #11
26. juni 2017 af fosfor

#8 Hvis den løsning skal gælde mangler der en begyndelsesværdi:
A(0) = 0
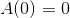
som må være givet eller følge af kontekst.

Start med ligningen for A_a

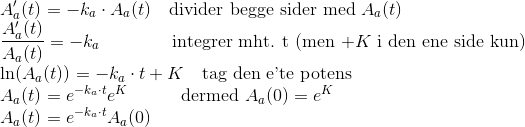
$\\A_a'(t)=-k_a\cdot A_a(t) \quad\text{divider begge sider med }A_a(t)\\ \frac{A_a'(t)}{A_a(t)}=-k_a\quad\quad\quad\quad \text{integrer mht. t (men +}K \text{ i den ene side kun)}\\ \ln(A_a(t))=-k_a\cdot t + K \quad\text{tag den e'te potens}\\ A_a(t)=e^{-k_a\cdot t}e^K \quad\quad\quad \text{dermed }A_a(0)=e^K\\ A_a(t)=e^{-k_a\cdot t}A_a(0)$

Og brug A_as form i den anden ligning

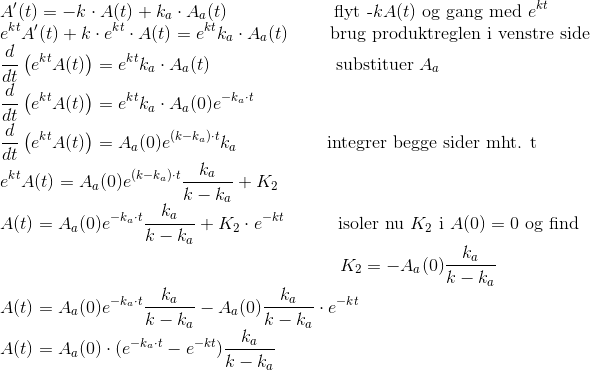
$\\A'(t)=-k\cdot A(t) + k_a \cdot A_a(t) \quad\quad\quad\quad\quad\quad \text{flyt -}k A(t)\text{ og gang med }e^{kt}\\ e^{kt}A'(t)+k\cdot e^{kt}\cdot A(t)= e^{kt} k_a \cdot A_a(t) \quad\quad \text{ brug produktreglen i venstre side}\\ \frac{d}{dt}\left(e^{kt} A(t)\right)= e^{kt} k_a \cdot A_a(t) \quad\quad\quad\quad\quad\quad\quad \text{substituer }A_a\\ \frac{d}{dt}\left(e^{kt} A(t)\right)= e^{kt} k_a\cdot A_a(0)e^{-k_a\cdot t} \\ \frac{d}{dt}\left(e^{kt} A(t)\right)= A_a(0) e^{(k-k_a)\cdot t} k_a \quad\quad\quad\quad\quad\text{integrer begge sider mht. t}\\ e^{kt} A(t)= A_a(0) e^{(k-k_a)\cdot t} \frac{k_a}{k-k_a} +K_2\\ A(t)= A_a(0) e^{-k_a\cdot t} \frac{k_a}{k-k_a} +K_2\cdot e^{-kt}\quad\quad\quad\text{isoler nu }K_2\text{ i }A(0)=0\text{ og find}\\ \text{ }\hspace{7.7cm}K_2 = -A_a(0) \frac{k_a}{k-k_a}\\ A(t)= A_a(0) e^{-k_a\cdot t} \frac{k_a}{k-k_a} -A_a(0) \frac{k_a}{k-k_a}\cdot e^{-kt}\\ A(t)= A_a(0) \cdot (e^{-k_a\cdot t}-e^{-kt}) \frac{k_a}{k-k_a}$

Hvis du har andre differentialligninger, så kig evt. her (under "hand solution")
http://12000.org/my_notes/kamek/version_4/KEse2.htm#x4-30002

Skriv et svar til: Løsning til differentialligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.