Matematik

Integral regning

21. juli 2017 af sofiekner (Slettet) - Niveau: B-niveau

To funktioner f og g har forskrifterne f(x)=kvadratroden3x+9 og g(x)=x+3.
Graferne for f og g afgrænser i anden kvadrant en punktmængde M, der har et areal.

a) Bestem arealet af M.

For k > 0 afgrænser graferne for de to funktioner sammen med linjen med ligningen
x =k i første kvadrant en punktmængde N.

b) Bestem k, så arealerne af M og N er lige store.

jeg er lidt i tvivl om hvordan man skal løse opgave a. Jeg tænker at man skal starte med arealfunktionen for både f(x) og g(x). også trække dem fra hinanden. Er det rigtigt? nogen der kan hjælpe mig

Brugbart svar (0)

Svar #1
21. juli 2017 af SuneChr

a) Ja, det er rigtigt.
Find de to grafers to skæringspunkter med hinanden og benyt disse som integrationsgrænser.
Da f (x) "ligger øverst" skal man sige integralet af (f (x) - g (x))

Svar #2
21. juli 2017 af sofiekner (Slettet)

jeg får f(x) til -11,588 og g(x) til -13,500. Ser de rigtigt ud?

Brugbart svar (0)

Svar #3
21. juli 2017 af SuneChr

Du skal sige

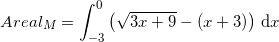
$\small Areal_{M}=\int_{-3}^{0}\left ( \sqrt{3x+9}-\left ( x+3 \right ) \right )\, \textup{d}x$

Brugbart svar (0)

Svar #4
21. juli 2017 af mathon

Brugbart svar (0)

Svar #5
21. juli 2017 af mathon

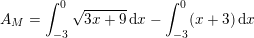
$\small A_M=\int_{-3}^{0}\sqrt{3x+9}\, \mathrm{d}x-\int_{-3}^{0}(x+3)\, \mathrm{d}x$

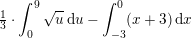
$\small \tfrac{1}{3}\cdot \int_{0}^{9}\sqrt{u}\, \mathrm{d}u-\int_{-3}^{0}(x+3)\, \mathrm{d}x$

Brugbart svar (0)

Svar #6
21. juli 2017 af mathon

$\small A_M=\tfrac{1}{3}\cdot \tfrac{2}{3}\cdot \left [ u\cdot \sqrt{u} \right ]_0^9-\left [\tfrac{1}{2}x^2+3x \right ]_{-3}^0=$

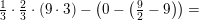
$\small \tfrac{1}{3}\cdot \tfrac{2}{3}\cdot \left ( 9\cdot 3 \right )-\left ( 0-\left ( \tfrac{9}{2}-9 \right ) \right )=$

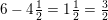
$\small 6-4\tfrac{1}{2}=1\tfrac{1}{2}=\tfrac{3}{2}$

Brugbart svar (0)

Svar #7
22. juli 2017 af mathon

b)
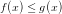        Da $\small f(x)\leq g(x)$ for $\small x\in \left [ 0; \infty\right ]$

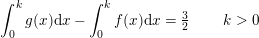        $\small \int_{0}^{k} g(x)\mathrm{d}x-\int_{0}^{k}f(x) \mathrm{d}x=\tfrac{3}{2}\; \; \; \; \; \; \; \; k>0$       ^{som du solver}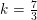

$\small k=\tfrac{7}{3}$

Brugbart svar (0)

Svar #8
22. juli 2017 af mathon

komtrolberegning:

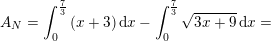
$\small \small A_N=\small \int_{0}^{\frac{7}{3}}\left ( x+3 \right )\mathrm{d}x-\int_{0}^{\frac{7}{3}} \sqrt{3x+9} \, \mathrm{d}x=$

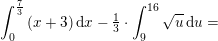
$\small \int_{0}^{\frac{7}{3}}\left ( x+3 \right )\mathrm{d}x-\tfrac{1}{3}\cdot \int_{9}^{16} \sqrt{u} \, \mathrm{d}u=$

$\small \left [\tfrac{1}{2}x^2+3x \right ]_0^{\frac{7}{3}}-\tfrac{2}{9}\cdot\left [ u\sqrt{u} \right ] _9^{16}=$

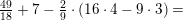
$\small \tfrac{49}{18}+7-\tfrac{2}{9}\cdot \left ( 16\cdot 4-9\cdot 3 \right )=$

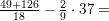
$\small \tfrac{49+126}{18}-\tfrac{2}{9}\cdot 37=$

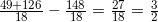
$\small \tfrac{49+126}{18}-\tfrac{148}{18}=\tfrac{27}{18}=\tfrac{3}{2}$

Brugbart svar (0)

Svar #9
22. juli 2017 af mathon

I
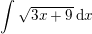$\small \int \sqrt{3x+9}\, \mathrm{d}x$ er anvendt substitutionen

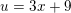$\small u=3x+9$ og dermed $\small \tfrac{1}{3}\mathrm{d}u=\mathrm{d}x$

Skriv et svar til: Integral regning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.