Matematik

Eksamensspørgsmål: differential og integralregning.

30. juli 2017 af randomdude11 (Slettet) - Niveau: B-niveau

Jeg skal besvare nedestående eksamenspørgsmål. Forslag og konstruktiv kritik er meget velkommen.

1."Redegøre for differentialkvotientbegrebet og sammenhængen mellem dette og stamfunktionsbegrebet."
beskrive tre trins reglen for et givet punkt og derigennem komme ind på differenskvotient, sekant, grænse værdi, tangent og differetialkvotienten. Og så snakke om Stamfunktioner som modstykket og beskrive integrationsprøven, ubestemt integral og bestemt.

2."forklar -på baggund af et konkret eksempel- hvordan man kan benytte disse i forbindelse med en beskrivelse af grafen for et polynomium. I din beskrivelse skal du bl.a. komme ind på monotoniforhold, ligninger for tangenter og arealer under ikke-negative grafer."

Jeg er forvirret over "ligninger for tangenter" er det ift. tangentsligningen eller andre differential kvotienter. Eller er det bare en forlængelse af monotoniforhold.
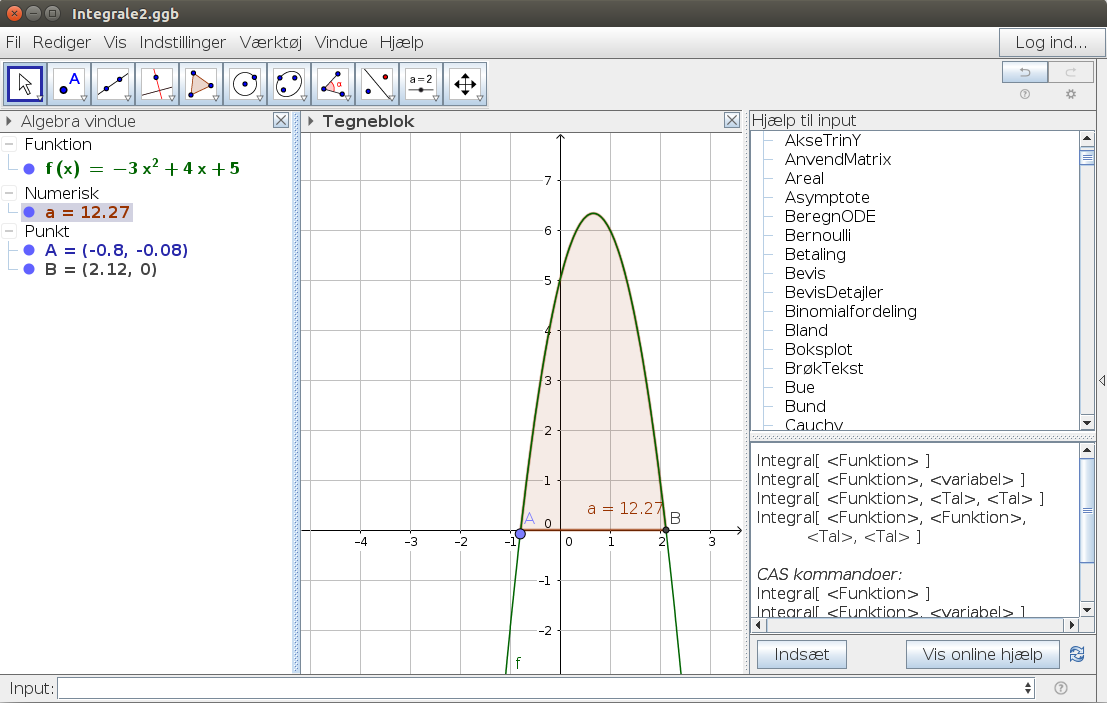
Ville funktionen 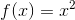f(x)=x^2 være dum, at bruge som eksempel.

3. Bevis tangentens ligning

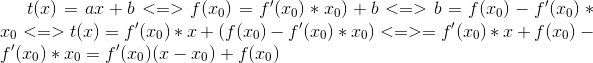
$t(x)=ax+b <=> f(x_{0})=f'(x_{0})*x_{0})+b <=> b=f(x_{0})-f'(x_{0})*x_{0} <=> t(x)=f'(x_{0})*x+(f(x_{0})-f'(x_{0})*x_{0})<=> =f'(x_{0})*x+f(x_{0})-f'(x_{0})*x_{0} =f'(x_{0})(x-x_{0})+f(x_{0})$

Brugbart svar (0)

Svar #1
30. juli 2017 af mathon

Tretrinsreglen er en beregningsmetode, som af pædagogiske grunde opdeles i tre trin.

Men det er tredje trin, der indeholder differentialkvotientbegrebet:

For en kontinuert funktion f(x)
defineres - forudsat den eksisterer -
grænseværdien:

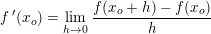$\small \small f{\, }'(x_o)=\underset{h\rightarrow 0}{\lim} \; \frac{f(x_o+h)-f(x_o)}{h}$ med betegnelsen differentialkvotienten i x_o.

Brugbart svar (0)

Svar #2
30. juli 2017 af mathon

2.
             Stamfunktionerne til den kontinuerte funktion f(x)
             er
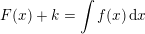
                              $\small \small F(x)+k=\int f(x)\, \mathrm{d}x$
             hvor der for 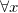$\small \forall x$ gælder:

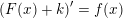
$\small \left (F(x)+k \right ){}'=f(x)$

Brugbart svar (0)

Svar #3
30. juli 2017 af mathon

3.
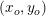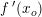     En tangent til grafen for f(x) er en ret linje gennem $\small \left ( x_o,y_o \right )$ med hældningstal $\small f{\, }'(x_o)$ ,
     for hvilken punkt-hældningsformlen
     giver:
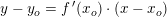
                      $\small y-y_o=f{\, }'(x_o)\cdot (x-x_o)$

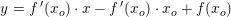
$\small y=f{\, }'(x_o)\cdot x-f{\, }'(x_o)\cdot x_o+f(x_o)$

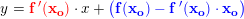
$\small y=\mathbf{\color{Red} f{\, }'(x_o)}\cdot x+\mathbf{\color{Blue} \left (f(x_o)-f{\, }'(x_o)\cdot x_o \right )}$

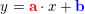
$\small y=\mathbf{\color{Red} a}\cdot x+\mathbf{\color{Blue} b}$

Brugbart svar (0)

Svar #4
30. juli 2017 af mathon

eks:

Brugbart svar (1)

Svar #5
30. juli 2017 af mathon

Ville funktionen 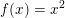$\small f(x)=x^2$ være "dum", at bruge som eksempel - JA lidt når du har frit valg..

Svar #6
30. juli 2017 af randomdude11 (Slettet)

#3
3.
     En tangent til grafen for f(x) er en ret linje gennem $\small \left ( x_o,y_o \right )$ med hældningstal $\small f{\, }'(x_o)$ ,
     for hvilken punkt-hældningsformlen
     giver:
                      $\small y-y_o=f{\, }'(x_o)\cdot (x-x_o)$

                      $\small y=f{\, }'(x_o)\cdot x-f{\, }'(x_o)\cdot x_o+f(x_o)$

                      $\small y=\mathbf{\color{Red} f{\, }'(x_o)}\cdot x+\mathbf{\color{Blue} \left (f(x_o)-f{\, }'(x_o)\cdot x_o \right )}$

                      $\small y=\mathbf{\color{Red} a}\cdot x+\mathbf{\color{Blue} b}$

I mit bevis har jeg ophævet parantesen og omskrevet det : 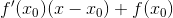$f'(x_{0})(x-x_{0})+f(x_{0})$ er det unødvendigt?

- "I din beskrivelse skal du bl.a. komme ind på monotoniforhold, ligninger for tangenter og arealer under ikke-negative grafer." Hvad er det, der menes med "ligninger for tangenter" helt præcis?

Brugbart svar (0)

Svar #7
30. juli 2017 af Number42

Bevis tangentens ligning:

tangenten er et ret linie som har et eller flere punkt tilfælles med kurven og hvor hældningen i et af punkterne er tilfælles med kurven i tangentpunktet.

y = a x +b er lignningen for en ret linie. liniens hældning er a som skal være lig kurvens hældning i punktet x₀

altså a = f'(x₀) ligeledes skal y(x₀) = f(x₀) = a x₀ + b hvilket giver y(x₀) = f'(x₀) x₀ +b hvoraf man finder b.

b = y(x0) - f'(x0) x0 = f(x₀) -f'(x₀) x₀

Den ligning kan med fordel også skrives: y = f'(x₀) ( x-x₀) +f(x₀) eller y = f'(x0) x + ( f(x₀)-f'(x0) x₀ ) eller

måske smukkest : f'(x₀) = (y-y(x₀)) / ( x-x₀ ) som tydeligt viser at tangenten har samme hældning som kurven

Mere kan man vist ikke få ud af " ligninger for tangenter"

Svar #8
30. juli 2017 af randomdude11 (Slettet)

#7
Bevis tangentens ligning:

tangenten er et ret linie som har et eller flere punkt tilfælles med kurven og hvor hældningen i et af punkterne er tilfælles med kurven i tangentpunktet.

y = a x +b er lignningen for en ret linie. liniens hældning er a som skal være lig kurvens hældning i punktet x₀

altså a = f'(x₀) ligeledes skal y(x₀) = f(x₀) = a x₀ + b hvilket giver y(x₀) = f'(x₀) x₀ +b hvoraf man finder b.

b = y(x0) - f'(x0) x0 = f(x₀) -f'(x₀) x₀

Den ligning kan med fordel også skrives: y = f'(x₀) ( x-x₀) +f(x₀) eller y = f'(x0) x + ( f(x₀)-f'(x0) x₀ ) eller

måske smukkest : f'(x₀) = (y-y(x₀)) / ( x-x₀ ) som tydeligt viser at tangenten har samme hældning som kurven

Mere kan man vist ikke få ud af " ligninger for tangenter"

Tak, tak. Det at "ligninger for tangenter" står i flertal og der alligevel i spørgsmålet senere står "bevis tangens ligning" fik mig til, at tro der var noget andet i det.

Brugbart svar (0)

Svar #9
31. juli 2017 af mathon

tangenten er et ret linie som har et eller flere punkt tilfælles med kurven og hvor hældningen i et af punkterne er tilfælles med kurven i tangentpunktet.

…flere fællespunkter er det rene vrøvl!

Skriv et svar til: Eksamensspørgsmål: differential og integralregning.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.