Matematik
2.-gradsligning
Hejsa,
SIdder med en økonomiopgave.. Total revenue is defined by: TR = P·Q, where P is the price and Q is sale of goods.
A demand function is given
P = 1000 - Q
Opgaven beder mig om:
express TR as a function of Q and hence sketch a graph of TR against Q. What value of Q maximises total revenue and what is the corresponding price?
Jeg har indsat min P-værdi ind i den første formel for total revenue:
TR = (1000 - Q) · Q = 1000Q - Q2
Nu kan jeg så bruge formlen for en 2.-gradsligning, givet at jeg lige laver lidt om på ligningen... til at finde den værdi af Q der giver størst fortjeneste, meen når jeg så finder x til at være 1000, og indsætter 1000 på Q's plads så får jeg 0. Og jeg har fundet ud af at hvis jeg sælger 500 goods så er min fortjeneste maksimal... Men der foretog jeg lidt gætteværk og indtaste nogle random tal manuelt..
Kan nogen forklare om opgavens hensigt var at udnytte grafen og på baggrund af det konkludere at 500 er dér hvor TR er størst? Fordi lige nu, uden at have en graf, så var lidt af et gættearbejde..for mig..
Skriv et svar til: 2.-gradsligning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


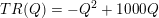 hvis graf er en grennedadvendende parabel
hvis graf er en grennedadvendende parabel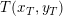
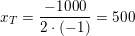 hvilket er den højst indbringende goods-mængde
hvilket er den højst indbringende goods-mængde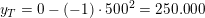 hvilket er
hvilket er 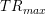 i kr.
i kr.