Matematik

Lipschitz function

20. september 2017 af Rossa - Niveau: Universitet/Videregående

Hej derude.
Jeg er bedt om at vise hvorfor to funktioner Lipschitz.
Funktionerne er:

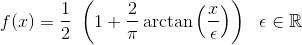
$f(x)= \frac{1}{2} \ \left( 1+ \frac{2}{\pi} \arctan\left(\frac{x}{\epsilon} \right ) \right ) \ \ \epsilon \in \mathbb{R}$

Normalt er epsilon en meget lille tal.
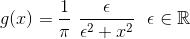
$g(x)= \frac{1}{\pi} \ \frac{\epsilon}{\epsilon^2+x^2} \ \ \epsilon \in \mathbb{R}$
Er 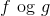$f \ \text{og} \ g$ Lipschitz function for en meget lille fikset værdi af $\epsilon$ ?
Hvad hvis 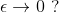$\epsilon \to 0 \ ?$

Det sværste er $\epsilon$ , der gør mig mest forvirret.
Det er ikke en opgave, men skal forstå argumenterne

Jeg håber, at nogen vil forklare det, og på forhånd tak

Brugbart svar (0)

Svar #1
21. september 2017 af Anders521

Hejsa,

ka' du minde os hvad definitionen er for en Lipschitz funktion.

Svar #2
21. september 2017 af Rossa

Jeg ville sige, at for et par punkter sige (x1, x2) , så vil
der gælde, at afstanden | f(x1) -f(x2) | < c |x1-x2 |
For c>0. Det skal også gælde ligheden, men kan ikke
Skrive via telefonen.

Brugbart svar (0)

Svar #3
21. september 2017 af Anders521

Men der er noget der mangler: hvor er dit epsilon henne? Men ... er der egentlig ikke tale om en vektor (x₁,x₂) som befinder sig i en omegn B(x₀, epsilon), hvor x₀ også er en vektor og B(x₀, epsilon) er et underrum af R^(n)?

Brugbart svar (0)

Svar #4
21. september 2017 af Therk

Hint: Kan du, for et givet (lille) epsilon finde et C så uligheden i #2 gælder?

Hint: Hvordan ser afbildingen 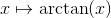ud for 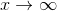$x\to \infty$ ? Den grænse svarer jo til dit lille epsilon (tænk at x/epsilon og y/epsilon er begge store tal).

Brugbart svar (0)

Svar #5
21. september 2017 af Tissemand020 (Slettet)

Slettet

Brugbart svar (1)

Svar #6
21. september 2017 af fosfor

Ifølge middelværdisætningen er findes x ∈ (x₁ ; x₂) så f'(x) = (f(x₂) - f(x₁)) / (x₂- x₁).
Ved at tage absolutværdi på begge sider fås |f'(x)| = |f(x₂) - f(x₁)| / |x₂ - x₁|.

Hvis f'(x) er begrænset |f'(x)| ≤ M har vi
|f(x₂) - f(x₁)| / |x₂ - x₁| = |f'(x)| ≤ M => |f(x₂) - f(x₁)| ≤ M |x₂ - x₁|

Dvs. hvis M = sup(|f '|) er endelig, så er f lipshitsz med konstant M

Svar #7
21. september 2017 af Rossa

Tusind tak :-). Det er lavet en opgave, og nu kan det forståes meget nemt. Tak igen

Skriv et svar til: Lipschitz function

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.