Grænseværdi
Hvad er en grænseværdi?
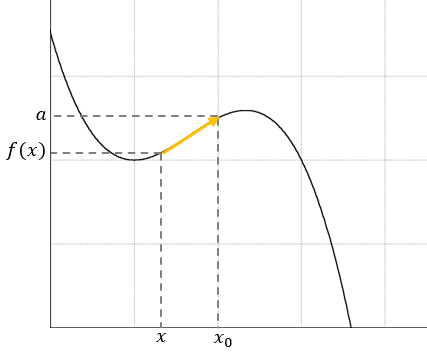
Når a er grænseværdi for f for x gående mod x0, så kan vi få en funktionsværdi vilkårligt tæt på a ved at vælge x tilstrækkeligt tæt på x0.
Vi betegner kun a som grænseværdi for f for x gående mod x0, hvis funktionsværdierne nærmer sig a for x gående mod x0 både fra venstre og fra højre.
Eksempel: Aflæs grænseværdien
Herunder ses grafen for funktionen f(x) = x2. Vi vil aflæse grænseværdien for f for x gående mod 2.
.png)
Vi aflæser på figuren, at når x går mod 2 fra venstre (blå pil), så vokser funktionsværdierne mod 4. Vi aflæser også, at når x går mod 2 fra højre (gul pil), så aftager funktionsværdierne mod 4. Uanset om vi lader x gå mod 2 fra venstre eller fra højre, så går funktionsværdierne altså mod 4. Grænseværdien for f for x gående mod 2 er derfor 4.
Grænseværdien eksisterer ikke altid
Hvis ikke funktionsværdie...

