Lineær sammenhæng
En lineær sammenhæng er tæt knyttet sammen med en lineær funktion og linjens ligning. Den grafiske afbildning for en lineær sammenhæng er nemlig en ret linje, ligesom de to førstnævnte. Mange lineære sammenhænge er ofte logisk åbenlyse.
Det mest simple eksempel er en lineær sammenhæng mellem antal og samlet pris. Én magnum-is koster 22 kr., to stk. magnum-is koster 44 kr., tre stk. magnum-is koster 66 kr. osv. Men der findes også mange lineære sammenhænge, som man ikke lige ville finde med blot den logiske sans.
En lineær sammenhæng undersøger om, og beskriver hvordan, to variable (x og y) hænger sammen. Som eksempelvis antal is (x) og samlet pris (y). Når der er en lineær sammenhæng, kan der i et koordinatsystem tegnes en ret linje.
Man vil ofte møde begrebet lineær sammenhæng, når man skal undersøge, om et antal koordinatsæt kan udtrykkes på formlen: y = ax + b eller f(x) = ax + b.
I en lineær sammenhæng er der en konstant a gange en uafhængig variabel x. Derudover kan der optræde en konstant b, der skal lægges til (eller trækkes fra) for at finde værdien af den afhængige variabel y. Således er den ene variabel er en lineær funktion af den anden variabel. Der er utallige variationer af lineære sammenhænge. Man kan stille sig selv den opgave at overveje, hvad der kan være en lineær sammenhæng.
Eksempelvis om der er en lineær sammenhæng mellem antallet af videregående uddannelser(x) og antallet af studerende på de videregående uddannelser (y)? Eller er der en lineær sammenhæng mellem antallet af kvindelige medlemmer af folketinget (x) og antallet af kvinder i bestyrelser (y)?
En lineær sammenhæng fordrer, at alle punkter i et givet talsæt grafisk placerer sig på en ret linje. Lad os se på et eksempel:
Eksempel 1
Fire husstande i en opgang får en elregning for deres kvartalsvise forbrug af el i november, december og januar. De betaler alle forskellige beløb, men husstandenes størrelser varierer også meget. Er der en lineær sammenhæng mellem den pris de fire husstande betaler og deres forbrug?
Herunder er opgjort det antal kWh (kilo-Watt-timer), som hver husstand har brugt og deres regning:
Husstand 1: 100 kWh = 4.537 kr.
Husstand 2: 200 kWh = 9.024 kr.
Husstand 3: 160 kWh = 7.229,20 kr.
Husstand 4: 210 kWh = 9.472,70 kr.
De fleste mennesker vil nok rent logisk forvente, at der er en lineær sammenhæng mellem elforbrug og pris, så alle elkunder betaler det samme pr. enhed. Lad os se på det ved at indtegne de fire koordinatsæt, der fremkommer ved at kombinere elforbrug og pris. Derved kan det kontrolleres, om der rent faktisk er tale om en lineær sammenhæng.
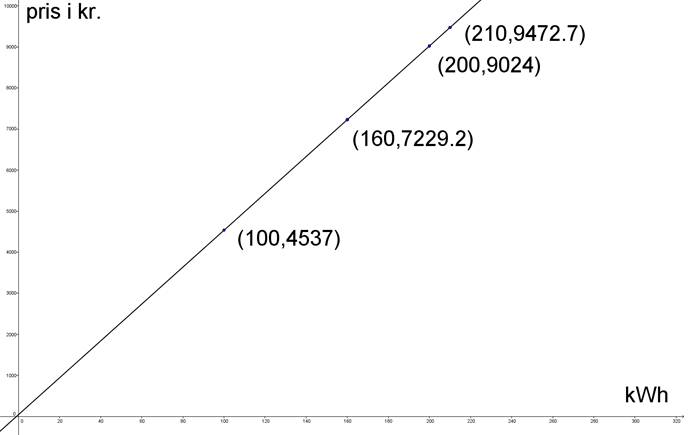
Som det fremgår, er de fire punkter alle på en ret linje, og der er derfor en lineær sammenhæng mellem elforbrug og pris.
For sjov skyld kan vi udregne linjens ligning ved hjælp af to punkter 

Så kan b bestemmes ud fra denne formel (man kan selv bestemme, hvilket punkt man indsætter):
Det kan være svært at se på figuren, men da b = 50 skærer grafen y-aksen i punktet (0,50).
Til sidst kan a og b indsættes i linjens ligning:
Det kan konkluderes, at der er en lineær sammenhæng mellem elforbrug (x) og pris (y), samt at elkunderne betaler 44,87 kr./kWh og at de derudover betaler 50 kr. i abonnement. Se endvidere artiklen lineær vækst.
Eksempel 2
5 personer, John, Karoline, Louise, Michael og Nikolaj, har vagt sammen som tjenere på en café. Det er kutyme, at tjenerne hver dag gør drikkepengene op, og deler dem ud til dem, der har været på arbejde den dag. Den pågældende dag har de fået 950 kr. i drikkepenge.
John, Louise og Michael møder kl. 10. Karoline møder kl. 12 og Nikolaj kl. 13. Normalt har de alle fri kl 21, men i dag går John kl 20. Da klokken nærmer sig 21 er alle gæster ikke gået, så Louise bliver og lukker og slukker. Hun ender med at få fri kl 22. Er der tale om en lineær sammenhæng mellem antal timer og de drikkepenge, de får med hjem, når de fordeles således:
John har haft 10 timer (10-20) og får 190 kr. i drikkepenge.
Karoline har haft 9 timer (12-21) og får 171 kr. i drikkepenge.
Louise har haft 12 timer (10-22) og får 228 kr. i drikkepenge.
Michael har haft 11 timer (10-21) og får 209 kr. i drikkepenge.
Nikolaj har haft 8 timer og (13-21) og får 152 kr. i drikkepenge.
For at kontrollere om der er tale om en lineær sammenhæng indtegnes punkterne (timer, drikkepenge) i et koordinatsystem.
.png)
Som det fremgår, ligger de fem punkter på en ret linje og der er derfor tale om en lineær sammenhæng mellem antal timer på vagt (x) og drikkepenge i kr. (y). Lad os i dette eksempel også udregne linjens ligning denne gang med en lidt anden metode.
Først skal a beregnes ligesom i eksempel 1 ved hjælp af to punkter, 

Nu indsættes a, i modsætning til eksempel 1, direkte i ’formlen for linjens ligning’, da man kender et punkt P

Tjenerne kan derfor regne ud, at for hver time de arbejder, får de 19 kr. oveni deres normale løn i drikkepenge. Da drikkepengene hver aften gøres op, er det samtidig logisk, at b = 0, og den lineære funktion derfor går gennem origo (0,0).
Alternativ
De fem tjenere kunne også have fordelt deres 950 kr. i drikkepenge i hele 10’ere og fordelingen ville da være:
John får 190 kr., Karoline får 170 kr., Louise får 230 kr., Michael får 210 kr. og Nikolaj får 150 kr.
Det ville se således ud på en grafisk afbildning og igen være en lineær sammenhæng.
.png)
Denne fordeling mellem timer og drikkepenge er, som beskrevet, en lineær sammenhæng, dog en lille smule mindre fair og lidt mere kompliceret.
Forskriften for denne lineære sammenhæng kan udregnes til at være:
y = 20x – 10
I praksis vil det sige, at de denne dag får 20 kr. i drikkepenge pr. time (x) minus et fast beløb på 10 kr. i en slags startgebyr. Det er mærkeligt - men stadig en lineær sammenhæng.
For John går det lige op. For dem, der arbejder mindre end John, er det en dårligere fordeling, for dem, der arbejder mere end John, er det en bedre fordeling. Dog er det minimale forskelle, da de alle fem arbejder stort set lige meget.
Havde de fem tjenere fordelt pengene mellem sig i fem lige store bidder 950\) kr.\5 = 190 kr. til hver, havde der IGEN været tale om en lineær funktion mellem timer og drikkepenge.
I det tilfælde ville a = 0 og derfor ville denne lineære funktion være en konstant funktion. Grafisk en vandret linje med forskriften y = 190.






