Linjens ligning

Linjens ligning beskriver i bund og grund det samme som en lineær funktion. Men i linjens ligning er (f(x) byttet ud med y. Linjens ligning er således den matematiske betegnelse for en ret linje med konstant hældning. Denne kan altid afbildes grafisk som en ret linje i et koordinatsystem.

I linjens ligning indgår to konstanter (a) og (b) samt to variable. x er den uafhængige variabel og y er den afhængige variabel. På samme måde som en lineær funktion defineres som f(x) = ax + b, kan linjens ligning opstilles på følgende formel:

y er den afhængige variabel og beskriver y-koordinatet

x er den uafhængige variabel og beskriver x-koordinatet

a er en konstant og linjens hældning der beskriver hvor stejl linjen er

b er en konstant og udtryk for linjens skæringspunkt med y-aksen

Herunder ses et ekempel på linjens ligning og den grafiske afbildning. Linjens ligning for ½x + 1

Hældning

For betydningen af hældningen a i linjens ligning, se artiklen hældningskoefficient.

Skæringspunkt med y-akse

Som beskrevet ovenfor kan man ud fra linjens ligning se at b = 1. Skæringspunkt med y-aksen har pr. definition 0 som det første koordinat. b i linjens ligning er altid det andet koordinat.

Derfor går skæringspunkt med y-aksen pr. definition igennem punktet .

Det fremgår af punktet  på figuren, idet linjen  skærer y-aksen i det punkt.

Når b =  går linjen gennem origo .

En linje der går igennem origo kaldes ligefrem proportional.

Skæringspunkt med x-akse

Når man skal finde en linjes skæring med x-aksen, skal man sætte . Det skyldes at , er sammenfaldende med x-aksen. 

Man indsætter derefter i linjens ligning, og kan nu isolere x. Skæringspunktet med x-aksen har pr. definition 0 som det andet koordinat.

Eksempelvis vil man undersøge hvor linjen \ ½x + 1 skærer x-aksen?

  

  

  

Dermed skærer linjen  x-aksen i punktet , som man også kan se på figuren ovenfor.

Linjens ligning ud fra to punkter

Linjens ligning kan bestemmes, blot man kender to punkters koordinatsæt,  og , og man ved at der et tale om en lineær sammenhæng.

De to punkters koordinatsæt og  benyttes først til at finde hældningen a for linjens ligning ud fra følgende formel:

Find derefter b ud fra følgende formel (man kan selv bestemme, hvilket af de to punkters koordinatsæt man indsætter):

el.

Når man har fundet både a og b skal de blot indsættes i linjens ligning .

Eksempel 1

Lad os se på et eksempel hvor de to punkter  og  er udtryk for en lineær sammenhæng (og lineær vækst):

For at finde linjens ligning skal hældningen a først udregnes:

 ⇒  ⇒  ⇒ a = ½

Derefter udregnes b ved hjælp af punktet  og a:

 ⇒  ⇒  ⇒ b = -2

De fundne værdier for a og b kan nu indsættes i linjens ligning:

y = ax + b ⇒ y = ½x  – 2

Den lineære sammenhæng, hvor punkterne  og  indgår, er dermed bestemt ved linjens ligning:

y = ½x – 2

Hvis man ville finde flere koordinatsæt, kunne de findes ved hjælp af et sildeben.

Linjens ligning ud fra hældning og et punkt

Linjens ligning kan i naturlig forlængelse af ovenstående bestemmes, når man kender hældningen og et punkt. En ret linje med hældningen a, der går igennem punktet  kan bestemmes ud fra ’formlen for linjens ligning':

Eksempel 2

En ret linje har hældningen  og går igennem punktet 

Formlen for linjens ligning kan nu bestemmes udfra 

 ⇒  ⇒ 

Linjens ligning ud fra vinkel med x-akse og punkt

Kender man en ret linjes vinkel v med x-aksen samt et punkt P, kan linjens ligning bestemmes. Når man kender punktet , skal man blot udregne hældningen a for at kunne indsætte i formlen for linjens ligning. Hældningen a er defineret som:

Eksempel 3

En ret linje danner en vinkel v = 63,43^° med x-aksen og går igennem punktet P(5,0).

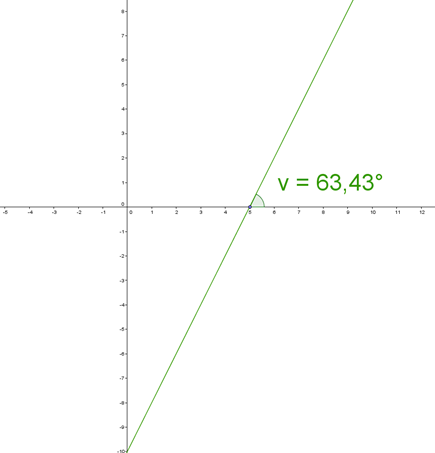
Først beregnes hældningen a:

 ⇒  ⇒  ≈ 2,00

Afrundet til 2 decimaler kan hældningen a og punktet P nu indsættes i formlen for linjens ligning: 

 ⇒ 

Vinklen med x-aksen tilsvarer i øvrigt vinklen med en hvilken som helst vandret linje.