Momsberegning
Momsberegning er et eksempel på procentregning i praksis. Momsberegning bliver derfor i høj grad brugt af mennesker i dagligdagen. Især af alle de forretningsdrivende der skal pålægge moms på deres varer er beregning af moms helt afgørende at mestre.
Alle danske varer er pålagt en moms på 25%. Når man ser en pris på en vare i en butik, er den oftest inklusiv (med) moms.
Men moms kan også være et yderligere tillæg til den pris, man får oplyst hos eksempelvis håndværkere (pris eksklusiv moms).
Prisen eksklusiv moms kaldes varens pris. Prisen inklusiv moms kaldes også varens totalpris.
Moms i Danmark
Har man en pris på 40 kr., skal man tillægge momsen på 25% for at finde totalprisen:
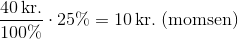
Totalprisen inklusiv moms bliver derfor:
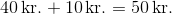
Man kan slippe for en mellemregning og lægge de 25 % til prisen med det samme.
Værdien er 40 kr., altså 100%. 25% er en delværdi af prisen, der skal lægges til.
Man skal gange med den oprindelige værdi plus delværdien for at finde den nye samlede pris. Ergo 100% + 25% = 125%:
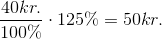
En anden måde at skrive det samme på:
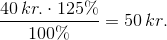
Her kan både tæller og nævner divideres med 100%:
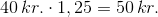
Det gælder derfor ALTID, at når man skal tillægge et beløb moms i Danmark:
Gang beløbet eksklusiv moms med 1,25
At tillægge moms svarer til en procentvis stigning i prisen fra 40 kr. til 50 kr. på 25%.
Udregning af moms når fuld pris kendes
I det modsatte tilfælde har man en totalpris inklusiv moms på 250 kr., hvor moms udgør 25%, men vil udregne prisen eksklusiv moms.
Igen kan man undgå en mellemregning, da det gælder, at momsen på 25% er lagt oveni (hele værdien plus delværdien: 100 % + 25 % = 125 %).
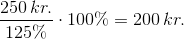
En anden måde at skrive det samme på:
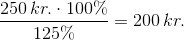
Her kan både tæller og nævner divideres med 125%:
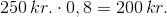
Prisen eksklusiv moms er 200 kr.
Moms udgør i kroner i dette tilfælde: 250 kr. - 200 kr. = 50 kr.
Eller i procent:

Sammenfattende kan det konkluderes, at når man skal finde prisen eksklusiv moms og dermed trække 20% fra totalprisen, svarer det ALTID til:
Gang beløbet inklusiv moms med 0,8
Momsregler
Konklusionen er altså, at når man i Danmark lægger 25% til en pris eksklusiv moms, modsvares det af at trække 20% fra prisen inklusiv moms.
Når man beregner, svarer det henholdsvis til at gange med 1,25 og gange med 0,8.
Der gælder følgende generelle regneregel for beregning af en totalpris inklusiv moms :
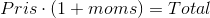
Der gælder følgende generelle regneregel for beregning af en pris eksklusiv moms :
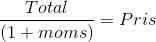
Eksempel 1
En virksomhed har udviklet et produkt, som de mener de skal have 70 kr. for, for at få profit. Denne pris er dog eksklusiv moms, så de bliver nødt til at lægge momsen oven i prisen, for at finde salgsprisen som kunderne skal betale.
Vi bruger vores formel til at regne ud hvor meget produktet skal koste for deres kunder:
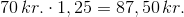
Virksomheden bliver altså nødt til at sætte prisen til 87,50 kr. for selv at få 70 kr. i indtægt per produkt, da de 17,50 er moms til staten.
Eksempel 2
En virksomhed vil udvide deres IT-afdeling med en ny computer. De finder en i et supermarked til 5500 kr. Denne pris er dog inklusiv moms, så virksomheden vil gerne regne ud hvor meget de skal betale eksklusiv moms.
Vi kan bruge reglen om trække momsen fra ved at gange med 0,8:
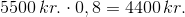
Virksomheden skal altså betale 4400 kr. eksklusiv moms for computeren.

