Procent til brøk
Procent til brøkomregning er ikke vanskeligt, da procent i forvejen kan ses som en brøk med 100 i nævneren.
Har man et procenttal, som man vil angive som brøk, skal man dividere med 100 %.
Eksempelvis 44 %:
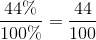
Det er oftest en fordel, fra procent til brøk, hvis man kan omregne til en såkaldt simpel brøk. Man skal som udgangspunkt angive den brøk, hvor nævneren er så lille som muligt i hele tal. Eksempelvis:

Har man derimod et procenttal med et komma, der skal angives som brøk, skal man foruden at dividere med 100% flytte kommaet, så man kan angive hele tal. Hvis der er to tal efter kommaet, skal man altså gange både tæller og nævner med 100. Eksempelvis 34,79%:

Ofte kan et kommatal være afrundet. For at kunne omskrive fra procent til brøk skal man være sikker på, at der ikke er sket en afrunding.
Vi vil nu kigge på nogle forskellige eksempler på omregning af procent til brøk.
Eksempel 1
I dette eksempel vil vi finde ud af, hvordan vi kan udtrykke 72 % som en brøk. Det første, vi gør, er at lave 72 % om til en hundrededele brøk:
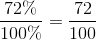
Næste skridt er at forkorte brøken så meget som muligt. Vi kan se at både tæller og nævner er lige tal, derfor kan vi forkorte brøken med 2:
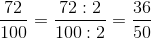
Vi har stadig to lige tal. Derfor kan vi forkorte med 2 igen:
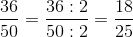
Vi har nu en nævner som er ulige og vi kan derfor ikke forkorte med 2 igen. Der kan dog stadig være fælles faktorer (tal der går op i) for tæller og nævner, så det er vigtigt at tjekke med andre tal.
Vi går altså igennem forskellige faktorer: 3 går op i 18 men ikke 25, 4 går ikke op i nogen af dem, 5 går ikke op 18, 6 går ikke op i 25, og så videre. Vi fandt ikke nogen tal at forkorte med, og derfor kan vi konkludere at brøken er helt forkortet.
Vi har altså at 72 % er lig 18/25 som brøk.
Eksempel 2
Lad os omregne 225 % til en brøk. Først dividerer vi med 100 %:
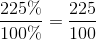
Her kan vi ikke forkorte med 2, da tælleren ikke er lige, men til gengæld kan vi forkorte med 25:

225 % er altså dette samme som 9/4. Vi bemærker at tæller er større end nævner. Afhængigt af formålet kan vi bruge denne brøk, som den er, men i mange tilfælde vil vi foretrække at skrive det som et blandet tal.
Man laver brøken om til et blandet tal, ved at se hvor mange gange nævner går op i tæller, og hvor meget der er tilbage af brøken derefter.
4 går 2 gange op i 9, og da 2 gange 4 er 8 er der 1/4 tilbage:
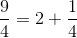
Man kan dermed sige, at 225 % er det samme som 2 og 1/4.
Eksempel 3
I dette sidste eksempel vil vi omregne 2,5 % til brøk.
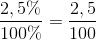
Da vi ikke kan have et kommatal i tælleren, bliver vi nødt til at forlænge. Da vi har 1 decimal efter kommaet, kan vi forlænge med 10 for at få et helt tal:
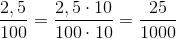
Nu skal vi dog lige tjekke, om vi kan forkorte. Igen ser vi, at vi kan forkorte med 25:
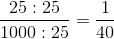
Altså 2,5 % er lig 1/40.

