Fremskrivningsfaktor og begyndelsesværdi
Fremskrivningsfaktoren a
En eksponentiel funktion er på formen
Tallet a kaldes grundtallet eller fremskrivningsfaktoren.
Når x vokser med 1, så bliver funktionsværdien a gange så stor. Som eksempel ser vi på funktionen f givet ved f(x) = 3 · 2x. Vi aflæser at a = 2, dvs. at funktionsværdien bliver 2 gange så stor, når x vokser med 1. Funktionsværdien fordobles altså, når x vokser med 1:
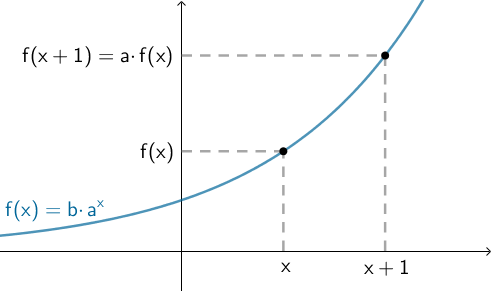
Vi kan vise, at når x vokser med 1, så bliver funktionsværdien a gange så stor ved at vise, at f(x + 1) er a gange så stor som f(x), dvs. at f(x + 1) = a · f(x).
 | = |  |
| = |  | |
| = |  |
Vi gennemgår, hvordan du kan fortolke konstanten a i en konkret kontekst i vejledningen Beskriv betydningen af konstanterne a og b, eller bestem vækstraten r.


![\begin{align*} f(0) &= 3 \cdot 2^0 \\[0.5em] &= 3 \cdot 1 \\[0.5em] &= 3 \\[1.5em] f(1) &= 3 \cdot 2^1 \\[0.5em] &= 3 \cdot 2 \\[0.5em] &= 6 \\[1.5em] f(2) &= 3 \cdot 2^2 \\[0.5em] &= 3 \cdot 4 \\[0.5em] &= 12 \\[1.5em] f(3) &= 3 \cdot 2^3 \\[0.5em] &= 3 \cdot 8 \\[0.5em] &= 24 \end{align*}](https://media.studienet.dk/files/webbooks/images/1981/equations/EvP80x0Grnk4J23peebdcA==.svg)
