Standardafvigelse
Standardafvigelse er et meget anvendt og nyttigt begreb i deskriptiv statistik. Standardafvigelse er en af de såkaldte statistiske deskriptorer.
Spredning er et andet ord for standardafvigelse. De to begreber, standardafvigelse og spredning, anvendes som synonymer i denne artikel.
Standardafvigelse betyder kort fortalt observationernes gennemsnitlige afvigelse fra middeltallet.
Spredning har én betydning for ugrupperede observationer og en anden for grupperede observationer, hvor observationerne er inddelt i intervaller.
Til at begynde med behandles spredning for ugrupperede observationer.
Den sidste del af artiklen omhandler spredning for de grupperede observationer.
Standardafvigelse kan ikke direkte aflæses, som eksempelvis typetal, median og variationsbredde, men skal beregnes.
Standardafvigelse benævnes med det græske bogstav σ (”lille sigma”). Standardafvigelse er defineret som kvadratroden af variansen.
På en formel ser det således ud.
Standardafvigelse formel
er standardafvigelse
er varians
Spredningen og variansen er, ligesom middeltal og median, statistiske deskriptorer der siger noget om middeltendensen i et observationssæt.
Især er middeltallet vigtigt for standardafvigelsen, da middeltallet indgår i formlen for varians og derfor også indirekte har betydning for spredningen.
Standardafvigelsen er for de fleste elever mere sigende end spredning til at forklare hvad der måles. Standardafvigelsen er således et mål for observationernes gennemsnitlige afvigelse fra middeltallet.
Lad os se på et par eksempler for at komme betydningen af standardafvigelse nærmere.
Eksempel 1
To elever har følgende fordeling af karakterer i 20 eksaminer angivet i frekvens:
| Karakter, x | Elev 1 | Elev 2 |
| 4 | f(x) = 10 % | f(x) = 40 % |
| 7 | f(x) = 40 % | f(x) = 10 % |
| 10 | f(x) = 40 % | f(x) = 10 % |
| 12 | f(x) = 10 % | f(x) = 40 % |
Standardafvigelse er defineret som kvadratroden af varians, som er beregnet på baggrund af middeltal. Se endvidere artiklerne Middeltal og Varians, for en mere udførlig beskrivelse.
Varians for elev 1 og elev 2 er udregnet til følgende:
V_elev 1 = 5,04
V_elev 2 = 13,37
Herefter kan spredning nemt beregnes.
Spredningen giver et billede af forskellen på de to elevers karakterfordelinger. Det giver også logisk mening, når man ser på karaktererne, at spredningen er større for elev 2 end for elev 1.
Eksempel 2
En person rejser ofte frem og tilbage mellem Århus og København.
| Pris i kr., x | Hyppighed, h(x) | Frekvens, f(x) |
| 160 | 5 | 0,50 = 50 % |
| 250 | 2 | 0,20 = 20 % |
| 404 | 3 | 0,30 = 30 % |
Se endvidere artiklen Middeltal for en mere udførlig beskrivelse.
Middeltal er beregnet til: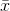 
= 251,20
Når man kender frekvens og middeltal kan varians bestemmes. Se artiklen Varians for udregning.
Varians er beregnet til: V = 11163,36
Herefter kan spredning nemt beregnes.
Dermed er spredningen for prisen på ture mellem Århus og København = 105,66 kr.
Standardafvigelse for grupperede observationer
Standardafvigelse for grupperede observationer er defineret lidt anderledes end for ugrupperede observationer.
Formlen er den samme, nemlig at standardafvigelsen: 
.
Men da middeltal og varians, der udgør grundlaget for standardafvigelse, udregnes på en lidt anden måde for grupperede observationer, er selve ’indmaden’ i formlen ovenfor anderledes for de grupperede observationer.
For grupperede observationer antager man nemlig, at de enkelte observationer ligger jævnt fordelt i intervallet og således fastsættes et intervalmidtpunkt, x_ midt for at beregne middeltal.
Samtidig er x_midt og f(I) indsat i formlen for varians, som man som bekendt skal tage kvadratroden af for at udregne spredningen, σ.
Skulle man opstille en formel for standardafvigelse for grupperede observationer ville den se således ud:
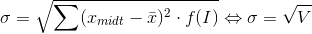
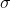er standardafvigelsen
x_midt er det fastsatte intervalmidtpunkt
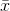er middeltallet
f(I) er intervalfrekvensen
V er variansen
Eksempel 3
Følgende datasæt, der viser aldersfordelingen af 25 børn i alderen 0 - 15 år, indgår i eksempel 3 i artiklen Varians.
|
Aldersinterval år |
Intervalhyppighed h(I) |
Intervalfrekvens f(I) |
Intervalmidtpunkt x_midt |
| 0 - 3 | 4 | 0,16 = 16 % | 1,5 |
| 4 - 6 | 5 | 0,20 = 20 % | 5 |
| 7 - 10 | 10 | 0,40 = 40 % | 8,5 |
| 11 - 15 | 6 | 0,24 = 24 % | 13 |
Middeltallet er beregnet til: 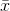= 7,76
Varians er beregnet til: V = 18,7712
Nu kan standardafvigelsen nemt beregnes, da den er defineret som kvadratroden af variansen.
Den standardafvigelse (gennemsnitlige spredning), der er fra middeltallet, er dermed lig med 4,3326 år eller ca. 4 år og 4 måneder.