Persondatapolitik

Studieportalen.dk › Kompendier › Matematik › Matematik formelsamling › Statistik › Deskriptiv statistik › Varians

Varians

Varians er et meget anvendeligt begreb i deskriptiv statistik, inferential statistik og sandsynlighedsregning.

Hvad er varians?

Inden for deskriptiv statistik er det korrekte navn faktisk ’empirisk varians’. Varians (alene) knytter sig i stedet til den inferentiale statistik. Glemmer man ’empirisk’, når man arbejder med deskriptiv statistik, kan varians dog godt stå alene betydningsmæssigt.

Varians er et mål for hvor meget observationerne i observationssættet i gennemsnit afviger fra middeltallet (middelværdien). Varians er en af de såkaldte statistiske deskriptorer.

For ugrupperede observationer har varians én betydning og for grupperede observationer, hvor observationerne er inddelt i intervaller, en anden.

Til at begynde med behandles varians for ugrupperede observationer. Den sidste del af artiklen omhandler varians for de grupperede observationer.

Varians må ikke forveksles med variationsbredde, da disse to statistiske deskriptorer er meget forskellige i betydning og anvendelse, trods deres enslydende navne.

Varians og spredning er knyttet tæt sammen, da kvadratroden af variansen er lig med spredning. Læs mere om spredning (standardsafvigelse).

Som beskrevet ovenfor knytter varians sig tættere sammen med middeltal og observationssættets middeltendens, hvorimod variationsbredde siger noget om observationssættets endepunkter. Se endvidere artiklen Boksplot.

Varians er IKKE en af de statistiske deskriptorer, der blot kan aflæses. Men varians for ugrupperede observationssæt kan nemt beregnes ved hjælp af nedenstående formel:

Varians-formel

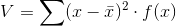
$V = \sum (x - \bar{x})^2 \cdot f(x)$

V er varians

x er de enkelte observationer

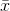$\bar{x}$ er middeltal

f(x) er frekvensen af de enkelte observationer

Dette lyder måske sværere og mere kompliceret end det i virkeligheden er. Lad os se på et par eksempler, da de kan være med til at øge overskueligheden og forståelsen for varians.

Eksempel 1

En person rejser ofte frem og tilbage mellem Århus og København. Dette ordnede observationssæt viser prisen på de seneste 10 ture:

160, 160, 160, 160, 160, 250, 250, 404, 404, 404

Pris Hyppighed Frekvens

160 5 0,50 = 50%

250 2 0,20 = 20%

404 3 0,30 = 30%

Middeltal beregnes til:

$\bar{x}$ = $((160 \cdot 0,50) + (250 \cdot 0,20) + (404 \cdot 0,30)) = 251,20$

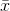Inden man kan udregne varians, skal man både kende frekvens og middeltal. Når de to statistiske deskriptorer er beregnet, kan varians bestemmes:

$V = (160 - 251,20)^2 \cdot 0,50 + (250 - 251,20)^2 \cdot 0,20 + (404 - 251,20)^2 \cdot 0,30 \Updownarrow V = 11163,36$

Dermed er varians for prisen på ture mellem Århus og København lig med 11163,36. Ikke en størrelse der siger én meget, men tallet giver straks mere mening, når man taler om standardafvigelse (spredning).

Eksempel 2

Her benyttes eksempel 3 fra artiklen Middeltal til at udregne varians for det samme observationssæt.

To elever får følgende fordeling af karakterer i 20 eksaminer, angivet med hyppighed og frekvens:

Karakter Elev 1 Elev 2

4: 2 = 0,10 8 = 0,40

7: 8 = 0,40 2 = 0,10

10: 8 = 0,40 2 = 0,10

12: 2 = 0,10 8 = 0,40

Sum: N = 20 N = 20

For elev 1 har vi udregnet at middeltal = 8,4, og for elev 2 er middeltal = 8,1.

Derefter kan varians udregnes med følgende formlen ovenfor:

$V_{elev 1} = (4 - 8,4)^2 \cdot 0,10 + (7 - 8,4)^2 \cdot 0,40 + (10 - 8,4)^2 \cdot 0,40 + (12 - 8,4)^2 \cdot 0,10 \Updownarrow V_{elev 1} = 5,04$

$V_{elev 2} = (4 - 8,1)^2 \cdot 0,40 + (7 - 8,1)^2 \cdot 0,10 + (10 - 8,1)^2 \cdot 0,10 + (12 - 8,1)^2 \cdot 0,40 \Updownarrow V_{elev 2} = 13,37$

Variansen viser, at der er stor forskel på de to elever, en forskel der yderligere uddybes i artiklen Standardafvigelse.

Varians for grupperede observationer

Varians for grupperede observationer er lidt anderledes defineret end for ugrupperede observationer.

For grupperede observationer antager man, at de enkelte observationer ligger jævnt fordelt i intervallet. Man fastsætter et intervalmidtpunkt, x_ midt, se artiklen om Middeltal for nærmere forklaring.

Beregning af varians for grupperede observationer foregår næsten på samme måde som for ugrupperede observationer. Blot skal x_ midt og f(I) indsættes, da det er intervaller der danner grundlag for beregningen af varians. Formlen ser således ud:

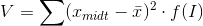
$V = \sum (x_{midt} - \bar{x})^2 \cdot f(I)$

V er variansen

x_midt er det fastsatte intervalmidtpunkt

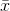$\bar{x}$ er middeltallet

f(I) er intervalfrekvensen

Eksempel 3

Fra eksempel 4 i artiklen Middeltal kender vi følgende datasæt om aldersfordelingen af 25 børn i alderen 0 - 15 år:

Aldersinterval, år	Intervalhyppighed	Intervalfrekvens f((I)
0 - 3	4	0,16 = 16 %
4 - 6	5	0,20 = 20 %
7 - 10	10	0,40 = 40 %
11 - 15	6	0,24 = 24 %

Derefter fastsættes et intervalmidtpunkt som en alder midt i intervallet:

0 - 3 år: x_midt = 1,5

4 - 6 år: x_midt = 5

7 - 10 år: x_midt = 8,5

11 - 15 år: x_midt = 13

Middeltallet er beregnet til 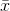$\bar{x}$ = 7,76

Variansen kan nu beregnes:

$V = (1,5 - 7,76)^2 \cdot 0,16 + (5 - 7,76)^2 \cdot 0,20 + (7,5 - 7,76)^2 \cdot 0,40 + (13 - 7,76)^2 \cdot 0,24 \Updownarrow V = 18,7712$

Varians siger i sig selv ikke så meget, men når man tager kvadratroden af V, og udregner standardafvigelse (spredning), giver det en mere håndgribelig information.

Seneste indlæg
9: Dansk mundligt (0)
9: Forsøg til vindmøller (bæredygti... (0)
B: Hjælp til differentialkvotienten... (2)
V: beregningsopgaver (0)
9: God måde til at finde Essays, Kl... (1)

Populære indlæg
9: lyrik please hjælp migggg!! (3)
9: Luther (3)
B: Hjælp til differentialkvotienten... (2)
A: vandtårn med hvor meget vand der... (10)
9: Dansk mundligt (0)

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se