Hvordan finder man arealet af en trekant?
Hvordan man finder arealet af en trekant, kommer an på hvilken type trekant man har at gøre med.
Alle trekanter bruger dog samme generelle formel for areal:
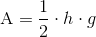
A er arealet. h er trekantens højde og g er trekantens grundlinje. Det kommer an på hvilken slags trekant man regner på, hvordan man måler højde og grundlinje. Grundlinjen vil altid være længden af en af trekantens sider, mens højden kun er lig en af sider hvis det er en retvinklet trekant.
Vi vil i denne artikel gennemgå en række eksempler med forskellige slags trekanter, hvor vi viser hvordan man finder arealet af trekanten. For en generel gennemgang se artiklen Areal af trekant.
Eksempel 1
Først vil vi finde arealet af en retvinklet trekant.
En retvinklet trekant er defineret ved at en af dens vinkler er ret (90 grader). Siden som ligger overfor den rette vinkel kalder vi for hypotenusen. De to andre sider, som rører hinanden i den rette vinkel, kaldes kateterne.
Eksempel på retvinklet trekant.
Denne trekant har en hypotenuse på 17 cm og to kateter på 8 cm og 15 cm.
En retvinklet trekant er nem at regne arealet på fordi højde og grundlinje bare er de to kateter.
Vi sætter ind i formlen:
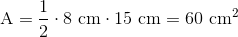
Denne retvinklede trekant har altså et areal på 60 cm2.
Eksempel 2
I dette eksempel vil vi finde arealet af en spidsvinklet trekant. En spidsvinklet trekant er defineret ved at alle dens vinkler er under 90 grader.
Eksempel på spidsvinklet trekant.
Når man har at gøre med en spidsvinklet trekant kan man ikke bruge en af siderne som højde, men må i stedet definere højden som en retvinklet linje, der går fra grundlinjen til vinklen overfor.
Grundlinjen definerer vi når mormalt som linjen der ligger nederst. Her er det derfor nemt at lave højde linjen, fordi den bare går ret op fra grundlinjen.
Vi har altså i dette eksempel en grundlinje på 10 cm og en højde på 8 cm. Vi sætter ind i formlen:
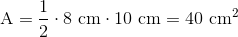
Denne spidsvinklede trekant har et areal på 40 cm2.
Eksempel 3
Vi vil nu kigge på en såkaldt stumpvinklet trekant. En stumpvinklet trekant har én vinkel som er over 90 grader.
Eksempel på stumpvinklet trekant.
I denne trekant giver det mest mening at lade den øverste side være grundlinjen. For at finde højden skal vi igen lade en linje gå ret ud fra grundlinjen, ud til den overfor stående vinkel.
Her er grundlinjen 12 cm lang og højden er 4 cm. Vi sætter ind i formlen:
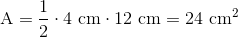
Denne stumpvinklede trekant har altså et areal på 24 cm2
Eksempel 4
I dette eksempel kigger vi igen på en stumpvinklet trekant. Denne ser dog anderledes ud.
Eksempel på stumpvinklet trekant, hvor højden ligger uden for trekanten.
Her har vi grundlinjen liggende så den vinkel som ligger overfor, ikke kan nås ved at gå ret op fra den. Derfor gør man det at man udvider grundlinjen indtil man kan gå lige op til vinklen.
Vi har markeret stykket der går ud fra grundlinjen med striplet linje. Det ekstra stykkes længde skal selvfølgelig ikke tælles med. Når man har udvidet grundlinjen er det nemt at tegne og måle højde.
Vi har altså en grundlinje på 7 cm og højde på 5 cm.
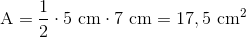
Trekanten har dermed et areal på 17,5 cm2.
Eksempel 5
I det sidste eksempel vil vi se på en ligebenet trekant
Eksempel på ligebenet trekant.
Ligebenede trekanter er defineret ved at to af siderne er lige lange, hvilket betyder at vinklen overfor grundlinjen altid vil være præcis i midten.
Derfor er det også rimelig ligetil at tegne højden. Det samme gælder for en ligesidet trekant, som er defineret ved at alle tre sider er lige lange.
Vi indsætter igen i formlen:
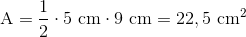
Denne ligebenede trekant har altså et areal på 22,5 cm2.






