Katete

En katete er en af siderne i en retvinklet trekant, som ligger omkring den rette vinkel.

Derfor har en retvinklet trekant altid to kateter, og de vil altid ligge vinkelret på hinanden.

Figuren viser hvad en katete er. De to kateter er markeret på en retvinklet trekant. Den rette vinkel er markeret med en firkant.

Den sidste side i trekanten kaldes hypotenusen.

Der er en række forhold, som gælder i en retvinklet trekant. En af de mest grundlæggende er Pythagoras' sætning:

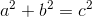
Her er a og b de to kateter, og c er hypotenusen. Sætningen siger altså, at kvadratet af den ene katete plus kvadratet af den anden katete er lig kvadratet af hypotenusen.

Man kan bruge længden af kateterne til at udregne længden af hypotenusen ved hjælp af Pythagoras' sætning - se artiklen Hypotenusen.

Et andet vigtigt forhold er mellem vinklerne og siderne i trekanten.

De trigonometriske funktioner kan defineres som forholdene mellem de forskellige sider i en retvinklet trekant.

Det første forhold er for cosinus:

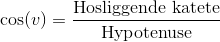
Denne sætning siger at for en vinkel v i en retvinklet trekant, er cosinus af v lig med den hosliggende katete divideret med hypotenusen.

Med den hosliggende katete menes der den katete, som ligger op til vinklen. Vinklen er altså mellem den hosliggende katete og hypotenusen.

Der gælder et lignende forhold for sinus:

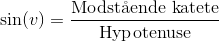
Altså sinus af v er lig den modstående katete divideret med hypotenusen. Her er den modstående logisk nok den katete, der ligger overfor vinklen.

Det sidste forhold, er forholdet mellem de to kateter:

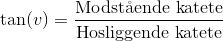
Tangens af en vinkel i en retvinklet trekant er altså lig den modstående katete divideret med den hosliggende katete.

Disse forhold er meget vigtige i matematik og kan for eksempel bruges, hvis man kender en vinkel og en side i en retvinklet trekant, men mangler at finde andre sidelængder.

Eksempel 1

I dette eksempel vil vi udregne længden af den ene katete i en retvinklet trekant.

Eksempel på retvinklet trekant.

Vi kender altså længden af én katete og hypotenusen, og vi skal finde længden af den anden katete.

Hvis vi kalder den ukendte katete b, ser Pythagoras' sætning således ud:

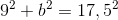
Vi skal altså isolere b:

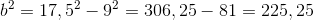
Vi tager kvadratet roden for at komme af med den anden potens.

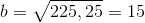
Kateten har altså en længde på 15 cm.

Eksempel 2

I dette eksempel vil vi udregne længde en katete ud fra den anden katete og en vinkel.

Retvinklet trekant hvor vi kender én katete og én vinkel.

Vi har her en trekant, hvor vi kender en vinkel 50 grader og længden på den hosliggende katete 10 cm.

Vi er interesseret i den modstående katete. Altså skal vi bruge formlen, der indeholder modstående og hosliggende katete, og det er formlen, der bruger tangens:

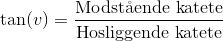
Vi isolerer den modstående katete og indsætter værdierne:

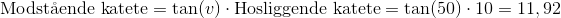
Den modstående katete i denne trekant er altså 11,92 cm lang.