Sinus og cosinus

Definition af cosinus og sinus

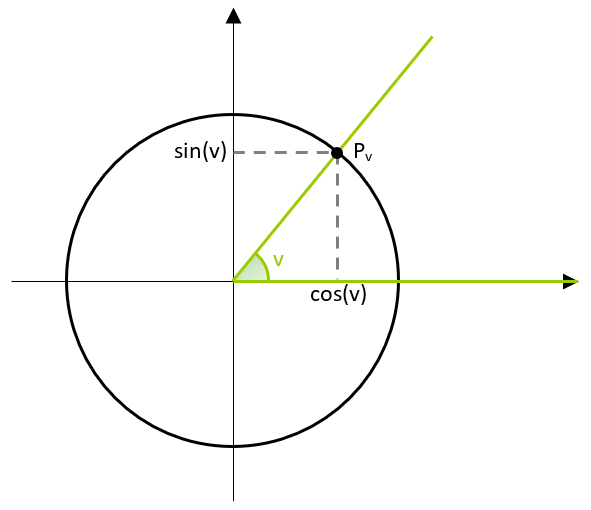
På figuren herover ses en vinkel v og det tilhørende retningspunkt Pv på enhedscirklen. Cosinus og sinus til vinklen defineres ud fra retningspunktet.

Da enhedscirklen har radius 1, så har alle punkterne på enhedscirklen første- og andenkoordinater i intervallet [-1,1]. Da cosinus og sinus er defineret som henholdsvis punkternes første- og andenkoordinater, så er

-1 ≤ cos⁡(v) ≤ 1

-1 ≤ sin⁡(v) ≤ 1

Vinklen v = 90° har retningspunktet Pv(0,1). Dermed er cos⁡(90°) = 0 og sin⁡(90°) = 1. Skemaet herunder viser en række vinkler (målt i grader og radianer) og de tilhørende værdier af cosinus og sinus.

Vinkel v

0°

30°

60°

90°

120°

150°

180°

210°

240°

270°

300°

330°

360°

Radiantal x

0

cos⁡(v)

1

0

-1

0

1

sin⁡(v)

0

1

0

-1

0

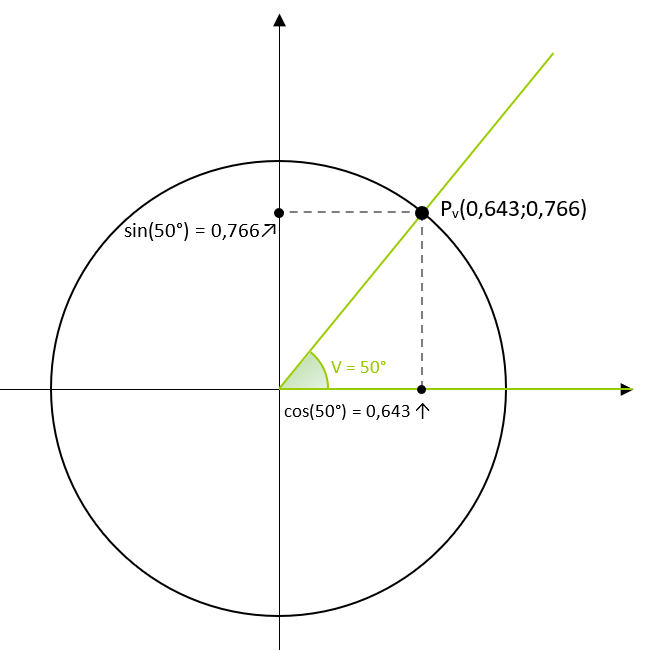
Eksempel: Bestem cos⁡(50°) og sin(50°)

På figuren herover har vi lagt vinklen v = 50° ind i et koordinatsystem sammen med enhedscirklen. Vi aflæser, at retningspunktets koordinater er (0,643;0,766). Da cosinus til vinklen er retningspunktets førstekoordinat, så er

cos⁡(50°) = 0,643...