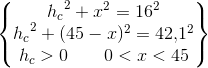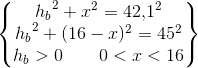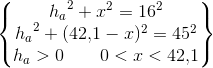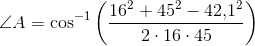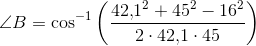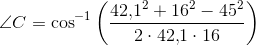Hvordan finder man højden i en trekant?

Du skal først og fremmest lave en tegning af trekanten med højden. Den behøver ikke at være nøjagtig. Find vinklerne i trekanten ved brug af cosinusrelationerne. Af tegningen kan du nu se at højden sammen med en af siderne udgør en retvinklet trekant, hvor du kender en side og 2 vinkler. Brug reglerne for trigonometriske funktioner i en retvinklet trekant til at finde højden. Præcis hvilken vinkler og sider du skal bruge er afhængig af hvilken højde, det drejer sig om.

Okay, mange tak (:

                  T = (1/4)·√(45² - (42,1-16)²) • √((42,1+16)² - 45²))

                  2T = (1/2)·√(45² - (42,1-16)²) • √((42,1+16)² - 45²)) ≈ 673,598

    og
                  h_1,2,3 = 2T/g_1,2,3

                                     • h₁ = 673,598/45    ≈ 15,0 

                                     • h₂ = 673,598/42,1 ≈ 16,0

                                     • h₃ = 673,598/16    ≈ 42,1

Hvad med bare at dele trekanten, så du kan bruge pythagoras' sætninge?

# 3

Kan det afsløres, hvad det er for en formel, du anvender i 1. linie - ?

Jeg tror, vi er mánge, der gerne vil forstå det tal-orgie ;-)

                     alment
                                        T = (1/4)·√(a² - (b-c)²) • √((b+c)² - a²))

                                        T = (1/4)·√(b² - (a-c)²) • √((a+c)² - b²))

                                        T = (1/4)·√(c² - (a-b)²) • √((a+b)² - c²))

# 6

Ikke mærkeligt, jeg undredes - jeg har aldrig set den formel før.

Da den ikke findes nogen af de forventede steder, vil du så oplyse, hvor den kan ses  (evt. udledningen) - ?

På forhånd tak -

                       Tjek den med Herons formel

                    s = (45 + 42,1 +16)/2  = 51,55

                    s-45 = 6,55

                    s - 42,1 = 9,45

                    s - 16 = 35,55

                    2T = 2·√(s·(s-a)·(s-b)·(s-c)) = 673,598

# 9

Selvfølgelig -

Det er så længe siden, jeg har brugt den formel, så den var næsten glemt (sig det ikke til Heron).

Men det havde været rigtig godt for os alle, hvis du lige havde nævnt navnet i # 3.

Tak ;-)

se udledning:
 

samt vinkelomskrivning

Udnytter lige muligheden til at spørge om hvordan man finder højden hvis man ved at i en trekant
Er A = 30 grader, og C = 90 grader. a = 11,5, b = 20, c = 23
er det a2 + b2 = c2, og derefter skal man tage kvadratroden af resultatet også har man fået højden ?? eller
 

# 13

Kald h_c's fodpunkt på c for D

Betragt trekant ADC
 

Vinkel ACD er 90-30=60 grader
 

h_c=BD=AC*cos(60)=20*cos(60)

@ #13:

der er noget inkonsistent i dine oplysninger

                                                                   a²               b²                  c²

                                                               11,5²             20²                23²

                                                              132,25     +    400               529

                                                                        532,025                    529

                                                             a² + b² ≠  c²        hvilket ikke er tilfældet i en trekant, hvor C = 90º

Okay, gode svar. tusinde tak for hjælpen !

undskyld jeg går stadigvæk i folkeskolen, kan du forklare, uden det er for kompliceret!!! det hele giver ikke mening for mig!!!! jeg vil bare find højden på den simpleste mode:-) hjæææælp mig nu!!!!!!

Det simpleste er omtalt i #1; men det forudsætter at du kender cosinusrelationerne. I beregninger med generelle trekanter skal du kunde nogle elementære formler, hvor cosinusrelationerne er en af dem

eller ligningssystemerne:
                                                  

med anvendelse af vinkler: