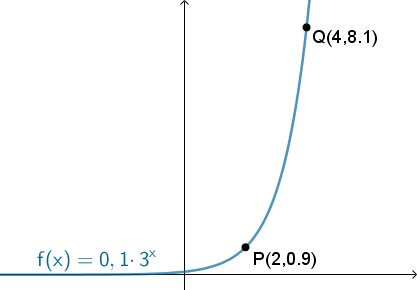
Eksponentielle funktioner
Her er vores kompendium om eksponentielle funktioner. Eksponentielle funktioner er en del af Matematik A, B og C på STX, HF, HHX og HTX.
Kompendiet indeholder bl.a. noter til eksponentielle funktioner og sider om eksamen. På siderne om eksamen kan du bl.a. få hjælp til at skrive emneopgave og til at øve typiske spørgsmål til samtaledelen af den mundtlige eksamen.

![\begin{align*} r_y &= a^{\Delta x} - 1 \\[0.5em] &= 3^2 - 1 \\[0.5em] &= 9 - 1 \\[0.5em] &= 8 \\[0.5em] &= 800\% \end{align*}](https://media.studienet.dk/files/webbooks/images/1981/equations/2oKhr9ztKOr9-Sf1NOP-LQ==.svg)