Bevis for fordoblingskonstanten

Her beviser vi formlen for fordoblingskonstanten T2:

$T_2 = \frac{\log(2)}{\log(a)} = \frac{\ln(2)}{\ln(a)}$

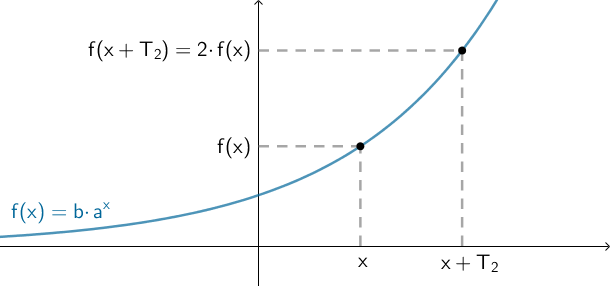
Alle eksponentielt voksende funktioner har en fordoblingskonstant. Fordoblingskonstanten er den værdi, som vi skal lægge til x, for at funktionsværdien bliver fordoblet, dvs. at

f(x + T2) = 2·f(x)

Sætning. Fordoblingskonstant.

Hvis f(x) = b·ax er en eksponentielt voksende funktion, dvs. at a > 1, så er fordoblingskonstanten T2 givet ved:

$T_2 = \frac{\log(2)}{\log(a)} = \frac{\ln(2)}{\ln(a)}$

Vi gennemgår et eksempel, hvor vi beregner fordoblingskonstanten for...

Teksten herover er et uddrag fra webbogen. Kun medlemmer kan læse hele indholdet.

Få adgang til hele Webbogen.

Som medlem på Studienet.dk får du adgang til alt indhold.

Køb medlemskab nu

Allerede medlem? Log ind